CTF竞赛中关于Coppersmith的考点,目前已经基本成为必考题之一,对于CTF新手来说,此知识点是必要掌握的。本文主要介绍 Coppersmith 应用 LLL 算法解决求解单变量模多项式方程小值解的方法。
关于Coppersmith
定理:设 N是一个未知因子分解的整数,$p \geq N^\beta$ 是 N 的一个因子,设 $f_p(x)$ 是一个单变量的次数为 $\delta$ 的多项式,设 $c_n$ 是一个以 $logN$ 为上界的量。那么我们可以在 $(logN,\delta)$ 的多项式时间内找到方程 $f_p(x) \equiv 0 \ mod \ p$ 的满足条件:$|x_0| \leq \frac{1}{2}N^{\frac{\beta^2}{\delta} - \varepsilon}$ 的解。
(这里的 $\varepsilon$ 是一个任意小的正数)
Coppersmith 方法的基本思路是将模多项式方程转化为整数上的多项式方程,利用 $f(x)$ 构造 $g(x)$ ,$g(x)$ 包含$f(x)$ 的所有小整数模根,即:$f(x_0) \equiv 0 (mod \ p) \Rightarrow g(x_0) = 0$
利用上面的定理容易证明:若 $N = p*q$ ,其中 p,q 是比特位相同的素数,那么已知 p 的 $\frac{1}{4} log_2N$ 高位(或低位)比特就可以在多项式时间内得到 N 的因子分解。
学习Coppersmith需要安装sagemath软件,推荐在ubantu中安装更加便捷。 接下来开始介绍利用 Coppersmith 定理解决RSA加密相关的问题。
对 sagemath 中用到的函数补充说明:
PolynomialRing :构造多项式环
Zmod(n) :模运算
implementation='NTL' :执行 NTL
small_roots(self, X=None , beta=1.0 , epsilon=None):计算多项式的小整数根
其中的参数:X —— 根的绝对边界, beta($\beta$) —— compute a root mod p where p is a factor of N and $p \geq N^\beta$
(程序默认值是 1.0 ,此时 p=N),epsilon (默认:$\beta/8$)
monic():用于将多项式的首项系数归一化为1。它接受一个多项式作为参数,然后返回一个新的多项式,其中首项系数已经被归一化为1。这个过程可以简化多项式的表达式,使其更易于计算和分析。
参考 sagemath文档介绍:后续在接下来的题目应用,讲解具体的用法。
已知素数p的高位攻击
在RSA加密算法中,如果私钥中的素因子泄露了部分信息,那么攻击者从这部分泄漏的数据中很可能会恢复出完整的私钥数据。设素因子 p 的二进制位表示为 :$pn ...p{t+1}p_t...p_1$ ,其高位比特数据 $pn ...p{t+1}$ 被泄露。令 $\Delta p = pn...p{t+1}0...0$ 为高位已知量, 设 $X = p_t...p_1$ 为低位未知量 , 由 $N=p*q$ 得:
$X$ 为模多项式 $f(x) = (\Delta p + X) \ mod \ N$ 的小整数解。
这里Coppersmith算法利用条件:知道 p 的高位为素因子p 的位数约 $\frac{1}{2}$ 比特位时即可。
例题:
from flag import flag
from Crypto.Util.number import *
p = getPrime(1024)
q = getPrime(1024)
e = 65537
n = p*q
m = bytes_to_long(flag)
print n
print pow(m, e, n)
print p>>256<<256
# output
# 26406507468595611843852094067483173843988114465094045314324958205247973393878612589146897816881236818219902539975703710689353618174826904300589643161784341674436810639999244652231756242284615955258973430337702733454791782484002773967293198343866259490519754466626455660967042613249021854707331393440280088268816341057924652807723419166490363777181753297185283416885627445213950857480287818564281651822264024891956284486733856518809532470029519647769749231421957169481281821885757924521580543834665554242403238567286205389138437021157096962185096308108489101554724344868500500476691994206988217768341711716527866730487
# 22371088752722216457725632164373582195669473128756299754645443284929524768654545905154985577175225182544638209286885657892360668965805613727315024761409924679131145149936406239774150607378706790494820180586939668429812955766507811860718575149988809217701964019618239260041070894375952033566803105327100696642244951676616707205397327491933042019560545721027871057909242509336729865025061616686254481161431063503607378134616485979961926628954536592552923269161255759846497309277397441639921544384778106116567555705005440627393593876072210594939647990615797269482726733444406876986888296295032722008287447468255108089357
# 159945952275533485818121954231313618960321976049710904254772419907677971914439101482974923293074598678164025819370654132149566696084245679106109087142916286461708005676333840438629476722637189134626565206159794947442549588155962485884562239895738265024295739578695834796427810095412842888401159276765814718464
这里我们已知素因子 p 的高位为 1024-256 = 768 bits ,未知的低位数据为 256 bits,根据上面的理论介绍我们可以使用 coppersmith 算法恢复 p的准确数据。
关键函数在于 small_roots 设置根的界限X 和 beta 的值,beat一般设置为 0.4 ,后面会详细介绍这样设置的目的。
x0 = p.small_roots(X=2^256,beta=0.4)
sagemath实现 exp :
#sage
from Crypto.Util.number import *
from gmpy2 import *
e = 65537
n = 26406507468595611843852094067483173843988114465094045314324958205247973393878612589146897816881236818219902539975703710689353618174826904300589643161784341674436810639999244652231756242284615955258973430337702733454791782484002773967293198343866259490519754466626455660967042613249021854707331393440280088268816341057924652807723419166490363777181753297185283416885627445213950857480287818564281651822264024891956284486733856518809532470029519647769749231421957169481281821885757924521580543834665554242403238567286205389138437021157096962185096308108489101554724344868500500476691994206988217768341711716527866730487
c = 22371088752722216457725632164373582195669473128756299754645443284929524768654545905154985577175225182544638209286885657892360668965805613727315024761409924679131145149936406239774150607378706790494820180586939668429812955766507811860718575149988809217701964019618239260041070894375952033566803105327100696642244951676616707205397327491933042019560545721027871057909242509336729865025061616686254481161431063503607378134616485979961926628954536592552923269161255759846497309277397441639921544384778106116567555705005440627393593876072210594939647990615797269482726733444406876986888296295032722008287447468255108089357
# print p>>256<<256
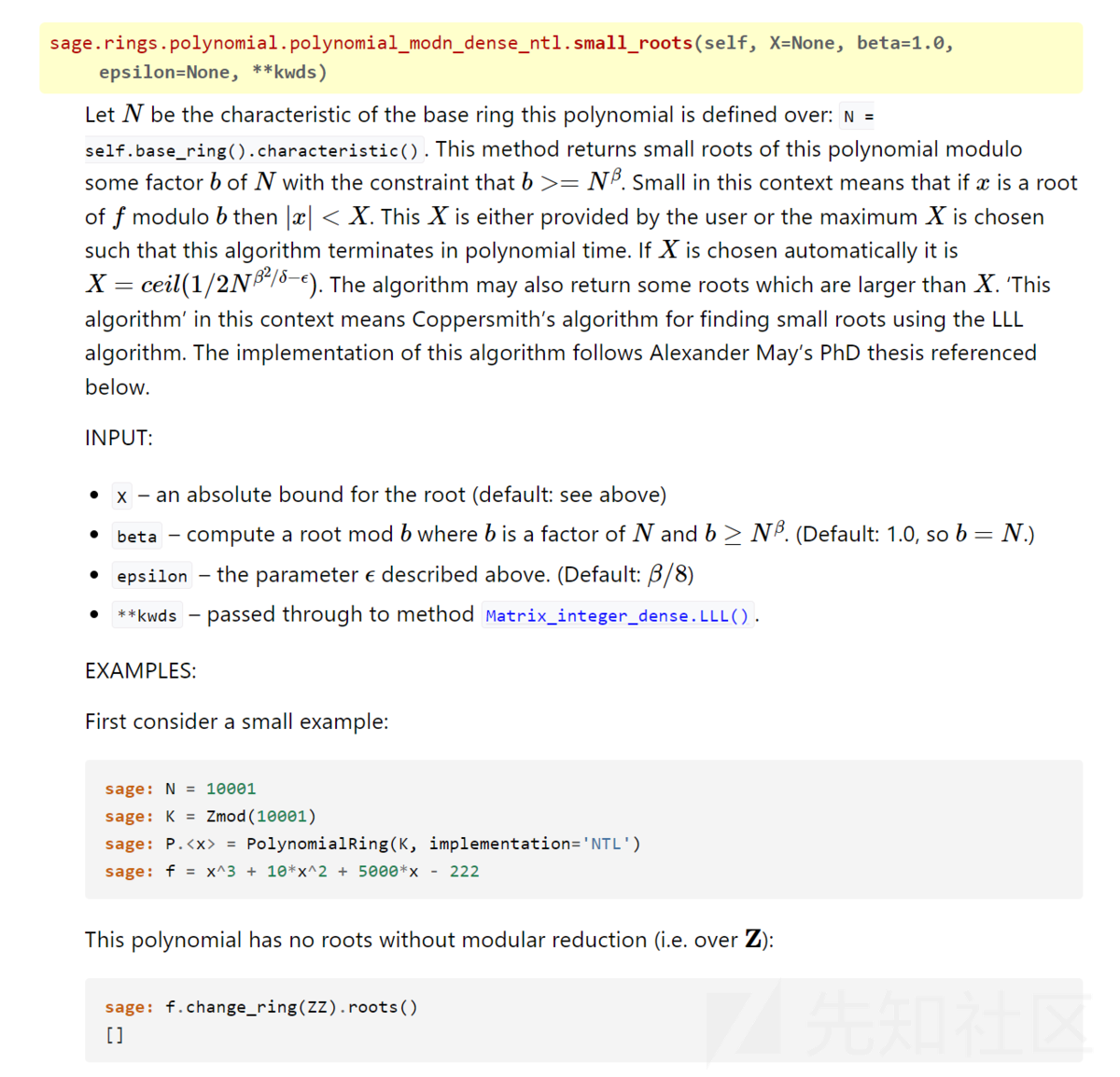
p_high = 159945952275533485818121954231313618960321976049710904254772419907677971914439101482974923293074598678164025819370654132149566696084245679106109087142916286461708005676333840438629476722637189134626565206159794947442549588155962485884562239895738265024295739578695834796427810095412842888401159276765814718464
PR.<x> = PolynomialRing(Zmod(n),implementation='NTL')
f = p_high + x
x0 = f.small_roots(X=2^256,beta=0.4)
print('x0 =',x0)
p = p_high + int(x0[0])
q = n//p
assert p*q==n
d = invert(e,(q-1)*(p-1))
m = pow(c,d,n)
print(long_to_bytes(int(m)))
sage中运算结果:得到模多项式的小整数根 $x_0$
x0 = [34617643142235695556586808773805798019055870312898061509976159971261415964273]
b'flag{f4f41143a6fc8f8f7365c6ccb5e3cb78}'
$x_0$ 也就是p的未知低比特位的值,将其与已知高比特位值相加即可:p = p_high + x0
注意这里的 p_high 缺失的低位填充成了 0 ,后面的 RSA 相关攻击算法也是一样的,如下图:
已知p的高位攻击(但高位不够的情况)
这里讲解两道题,都涉及到了当 p,q 同二进制位数时,已知 p 的高位攻击但高位不够的情况,在这里情况下,我们需要先爆破部分低位,使得未知低位满足条件:p_unknown_bits $\div$ p_bits $\leq 0.44$ (这里指beta = 0.44)
第一种情况
大家可以自己去生成一组 256 bits 或者更大数据量的素数 p,q 进行测试实验,如下是我已经测试过的结果:
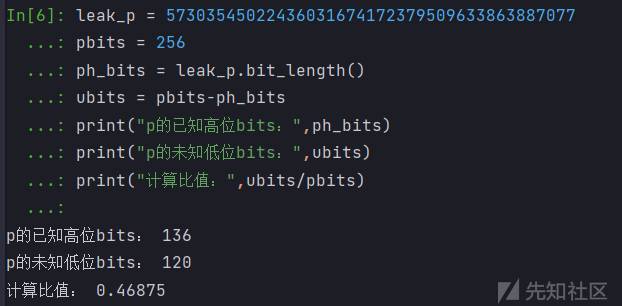
这样的数据直接拿去高位攻击是不行的,必须要已知 144 位才能高位攻击,
此时计算比值为 : (256 - 144) / 256 = 0.4375
我们要爆破 136 到 144 中的8位二进制数,即2位十六进制然后再进行已知高位攻击
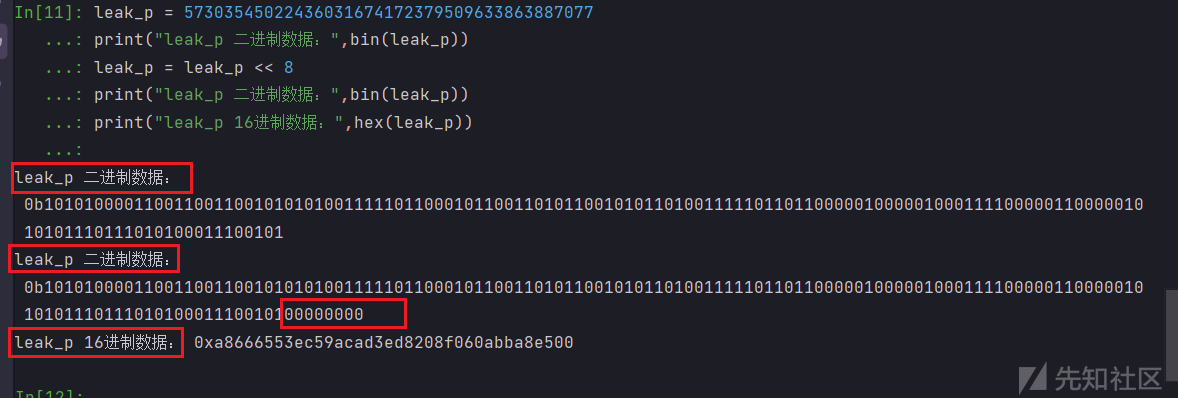
先将 leak_p 转化为16进制:
题目 task.py
from Crypto.Util.number import *
from gmpy2 import *
from secret import flag
m = bytes_to_long(flag)
e = 65537
p= getPrime(256)
leak_p = p >> 120
print("leak_p =",leak_p)
q = getPrime(256)
n = p*q
c= pow(m,e,n)
print("n =",n)
print("c =",c)
# leak_p = 57303545022436031674172379509633863887077
# n = 6290400850108673527783456723558868077251853788073859360516042680251422818079380463161520548743184302018140978345372703177688378631564416901363981788817257
# c = 3018879496435827891565409624549580574355607699876796814908055868300197064252462047054251836059387617618529706009316747223510404878163964048672091931778452
sagemath实现 exp :
from sage.all import *
from Crypto.Util.number import *
from gmpy2 import *
n = 6290400850108673527783456723558868077251853788073859360516042680251422818079380463161520548743184302018140978345372703177688378631564416901363981788817257
c = 3018879496435827891565409624549580574355607699876796814908055868300197064252462047054251836059387617618529706009316747223510404878163964048672091931778452
e = 65537
pbits = 256
# leak_p = 57303545022436031674172379509633863887077
# print(hex(leak_p<<8))
# leak_p = 0xa8666553ec59acad3ed8208f060abba8e500
for i in range(1, 127):
leak_p = 0xa8666553ec59acad3ed8208f060abba8e500
leak_p = leak_p + int(hex(i),16)
# print(leak_p)
kbits = pbits - leak_p.nbits() # 设置界的 bit上限
# print(kbits)
p_high = leak_p << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = p_high + x
roots = f.small_roots(X=2^kbits, beta=0.4) #计算模多项式的小整数根
if(roots):
print('roots =',roots)
p = p_high + int(roots[0])
q = n//int(p)
assert p*q == n
phi = (p-1)*(q-1)
d = invert(e,phi)
flag = int(pow(c,d,n))
print(long_to_bytes(flag))
这里采用的是循环爆破的方式,爆破出部分未知低比特位,然后再使用 coppersmith 算法计算模多项式的小整数根。
运算结果:
roots = [2302780466607342296780200504205035]
b'flag{b1695180-0205-461e-8f91-5474c719f5c6}'
第二种情况
第二种情况是不仅已知高位的位数不够,而且直接采用爆破部分低位再用coppersmith算法进行计算,也是行不通的,如直接采用这种写法:f.small_roots(X=2^253, beta=0.4)
这里用 [2023HGAME] CTF 的一道例题来讲解这种情况。
题目 task.py
def create_keypair(nbits):
p = getPrime(nbits // 2)
q = getPrime(nbits // 2)
N = p*q
phi = (p-1)*(q-1)
e = 65537
d = inverse(e, phi)
leak = p >> 253
return N, e, d, leak
#N = 115093328038628808000295235261362405802946414639474481950854274471056071400567939760489029514405676751158500439316121705879898379961723340037451609143927918592230719040332243486155308305995684632393529193889098207326916292333323740045854874108499021528070619818564785319040208958162851719315919939795936617311
#e = 65537
#leak = 724556813270353646000965587597160596427818318026275239319104891346445173041116
已知量为 N、e、leak,这里的 leak 为p泄露的高位值,未知低比特数为 253。
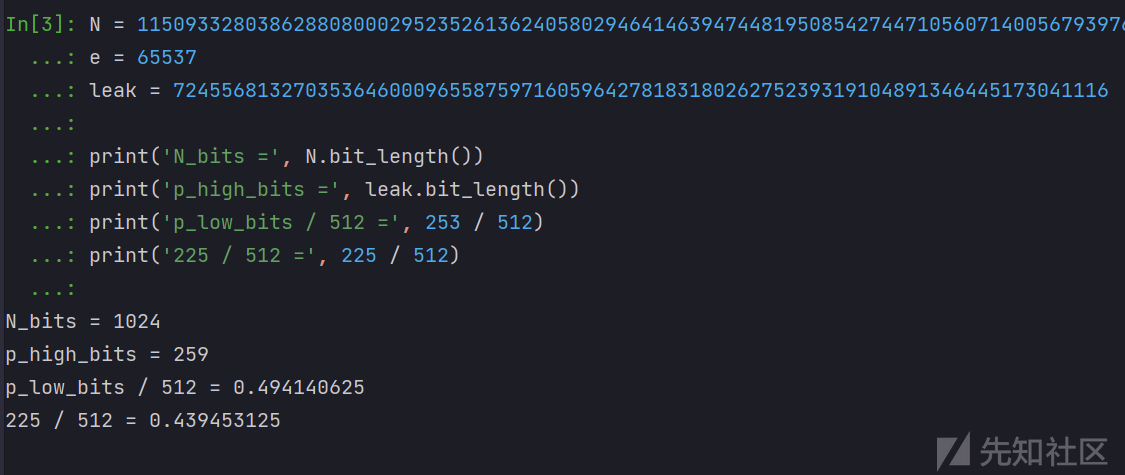
我们可以知道 N的大小为 1024 bits,p泄露的高位为 259 bits,未知的低位为 253 bits;按照公式前面理论部分的条件:p_unknown_bits $\div$ p_bits $\leq 0.44$ (这里指beta = 0.44),我们需要将 p 未知低位的数据量通过爆破降低到 225 bits 才可能通过 coppersmith算法计算出模多项式的小整数根。但爆破的数据量为 2^28 ,这用我们的计算机基本无法实现,也不是一个很好的方法。
改进我们的方法:
先爆破 p的低 10 位有效值,降低 未知低位bit/p_bits 的比值,然后利用 coppersmith 调节 $X$ 的边界,增大格的维度就能爆破出来了。边界的大小主要是通过调节small_roots 的参数 epsilon 的值,值越小,beta比值越接近或小于 0.44,同时随着调节的值越小计算速度会越慢。sage官方默认给的 epsilon = $\beta/8$,我们可以设置在0.01以上大一点。 关于爆破范围,这里取 2的9次方上下。也可能在 2的10次方附近。也就3、4分钟就出了,自己调节一下。这里我们设置为 f.small_roots(X=2 ^ kbits, beta=0.4,epsilon=0.015)
关于 sage.rings.polynomial.polynomial_modn_dense_ntl.small_roots(self , X=None , beta=1.0 , epsilon=None) 函数中参数更详细的介绍:
该函数是一个用于在整数模下搜索多项式小根的函数。该函数使用NTL库中的算法进行实现,并提供了一些参数来控制搜索的精度和效率。其中,
1、参数epsilon是一个可选参数,用于控制搜索多项式小根的精度。具体来说,epsilon用于控制NTL算法中使用的插值多项式的次数。插值多项式是一种多项式函数,可以通过一些已知的点来近似地计算一个函数在其他点上的值。在搜索多项式小根时,插值多项式用于确定多项式的根的近似位置。
当epsilon的值较小时,NTL算法使用的插值多项式次数也会比较小,这可以降低计算量,但可能会导致算法无法找到所有小根。相反,当epsilon的值较大时,NTL算法使用的插值多项式次数也会比较大,这可以增加算法找到所有小根的可能性,但计算量也会相应地增加。
需要注意的是,如果不指定epsilon参数,则NTL算法将使用默认值。默认情况下,epsilon的值为$\beta/8$。在实践中,这个值通常是比较合适的,但也可能需要根据具体情况进行调整。因此,在使用small_roots函数时,我们需要根据具体情况选择合适的epsilon值,以获得更准确的结果。
2、X:用于指定搜索多项式小根的范围。默认情况下,X的值为None,表示搜索整个整数域。如果需要限制搜索的范围,可以将X设置为一个正整数,表示搜索区间为$[-X, X]$。对于非常大的搜索范围,可以将X设置为一个RR对象,表示使用实数范围进行搜索。
3、beta:用于控制NTL算法中的松弛因子。松弛因子是一种通过调整插值多项式的精度来控制搜索速度和精度的方法。beta的默认值为1.0,表示使用默认的松弛因子。可以通过调整beta的值来改变算法的搜索速度和精度。较小的beta值会加快搜索速度,但可能会降低搜索精度,而较大的beta值则会增加搜索精度,但可能会降低搜索速度。
sagemath实现 exp :
from sage.all import *
from Crypto.Util.number import *
from gmpy2 import *
from tqdm import tqdm
e = 65537
n = 115093328038628808000295235261362405802946414639474481950854274471056071400567939760489029514405676751158500439316121705879898379961723340037451609143927918592230719040332243486155308305995684632393529193889098207326916292333323740045854874108499021528070619818564785319040208958162851719315919939795936617311
c = 0x8a887d3c9ee7f6ad81517ffbba417f5cac350abd3314b34d9f58845e15f68ef00fafb69ec0b60cdc90975c4db3f0fc1334f3fc9ed84c69e95fbb584a5f3158603523294ec3e79aea20080dd40513a6bd4532d8a64c1d46aae28fab19ea5b9d7aadea315c380ac9a2a92856af99204e79c6ea11b754e02db3f7c94efdb535cfe8
pbits = 512
# leak_p = 724556813270353646000965587597160596427818318026275239319104891346445173041116
# leak_p = leak_p<<10
# print(hex(leak_p))
# leak_p = 0x1907927e6c31e6d08b2d680921f7669fb4e9a15568cd3ed54a71d0861ff5629f7000
for i in tqdm(range(800, 1, -1)):
leak_p = 0x1907927e6c31e6d08b2d680921f7669fb4e9a15568cd3ed54a71d0861ff5629f7000
leak_p = leak_p + int(hex(i), 16)
# print(leak_p)
kbits = pbits - leak_p.nbits() # 用于设置根X的界限
# print(kbits)
p_high = leak_p << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = p_high + x
roots = f.small_roots(X=2 ^ kbits, beta=0.4, epsilon=0.015) # 计算模多项式的小整数根
if (roots):
print("p_root =", roots[0])
p = p_high + int(roots[0])
q = n // p
if p * q == n:
print("p =", p)
d = invert(e, (q - 1) * (p - 1))
m = pow(c, int(d), n)
print(long_to_bytes(int(m)))
运算结果:
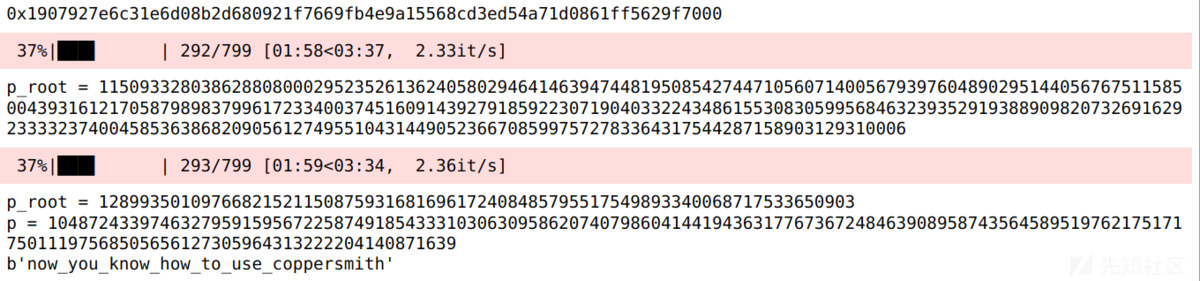
调节后可以看到计算出 flag 的速度还是很快的。
已知p的低位攻击
我们设素因子 p 的二进制位表示为 :$pn ...p{t+1}p_t...p_1$ ,其低位比特数据 $p_t ...p_1$ 被泄露。令 $\Delta p = p_t...p_1$ 为低位已知量, 设 $X = pn...p{t+1}$ 为高位未知量 , 由 $N=pq$ 得**:$X$ 为模多项式 $f(x) = (2^tX + \Delta p) \ mod \ N$ 的小整数解。**(其中的 t 就是 p 已知低位的比特数量)
例题 task.py:
from Crypto.Util.number import *
from secret import flag
p = getPrime(1024)
q = getPrime(1024)
n = p*q
m = bytes_to_long(flag)
e = 65537
c = pow(m, e, n)
print("n =", n)
print("c =", c)
print("p =", p&((1<<560) - 1))
'''
n = 21595945409392994055049935446570173194131443801801845658035469673666023560594683551197545038999238700810747167248724184844583697034436158042499504967916978621608536213230969406811902366916932032050583747070735750876593573387957847683066895725722366706359818941065483471589153682177234707645138490589285500875222568286916243861325846262164331536570517513524474322519145470883352586121892275861245291051589531534179640139953079522307426687782419075644619898733819937782418589025945603603989100805716550707637938272890461563518245458692411433603442554397633470070254229240718705126327921819662662201896576503865953330533
c = 1500765718465847687738186396037558689777598727005427859690647229619648539776087318379834790898189767401195002186003548094137654979353798325221367220839665289140547664641612525534203652911807047718681392766077895625388064095459224402032253429115181543725938853591119977152518616563668740574496233135226296439754690903570240135657268737729815911404733486976376064060345507410815912670147466261149162470191619474107592103882894806322239740349433710606063058160148571050855845964674224651003832579701204330216602742005466066589981707592861990283864753628591214636813639371477417319679603330973431803849304579330791040664
p = 1426723861968216959675536598409491243380171101180592446441649834738166786277745723654950385796320682900434611832789544257790278878742420696344225394624591657752431494779
'''
分析题目:
p = getPrime(1024)
print("p =", p&((1<<560) - 1))
从这两段代码可以得知:p = 1024bits,且 560 bits 低位数据是已知的,通过上面的理论知识我们可以构造相关的模多项式,然后利用 Coppersmith 算法计算出多项式的小整数根,即可恢复出完整的私钥 p。
用到的参数:monic():用于将多项式的首项系数归一化为1。
sagemath实现 exp :
#sage
from gmpy2 import *
from Crypto.Util.number import *
n = 21595945409392994055049935446570173194131443801801845658035469673666023560594683551197545038999238700810747167248724184844583697034436158042499504967916978621608536213230969406811902366916932032050583747070735750876593573387957847683066895725722366706359818941065483471589153682177234707645138490589285500875222568286916243861325846262164331536570517513524474322519145470883352586121892275861245291051589531534179640139953079522307426687782419075644619898733819937782418589025945603603989100805716550707637938272890461563518245458692411433603442554397633470070254229240718705126327921819662662201896576503865953330533
c = 1500765718465847687738186396037558689777598727005427859690647229619648539776087318379834790898189767401195002186003548094137654979353798325221367220839665289140547664641612525534203652911807047718681392766077895625388064095459224402032253429115181543725938853591119977152518616563668740574496233135226296439754690903570240135657268737729815911404733486976376064060345507410815912670147466261149162470191619474107592103882894806322239740349433710606063058160148571050855845964674224651003832579701204330216602742005466066589981707592861990283864753628591214636813639371477417319679603330973431803849304579330791040664
pbar = 1426723861968216959675536598409491243380171101180592446441649834738166786277745723654950385796320682900434611832789544257790278878742420696344225394624591657752431494779
PR.<x> = PolynomialRing(Zmod(n))
f = x*2^560 + pbar
f=f.monic()
kbit=1024-560 # 用于设置根X的界限
root = f.small_roots(X=2^kbit, beta=0.4,epsilon=0.015) # 计算模多项式的小整数根
p = int(2^560*root[0] + pbar)
q = n // p
assert p*q == n
e=65537
d=invert(e,(p-1)*(q-1))
m=pow(c,int(d),n)
print(long_to_bytes(int(m)))
已知明文m的高位攻击
在RSA加密算法中,如果泄露了部分明文信息,那么攻击者从这部分泄漏的数据中很可能会恢复出完整的明文。设明文 m 的二进制位表示为 :$mn ...m{k+1}m_k...m_1$ ,其低位比特数据 $mn ...m{k+1}$ 被泄露。令 $\Delta m = mn...m{k+1}0...0$ 为已知量, 设 $X = m_t...m_1$ 为未知量 ;由 $c \equiv m^e \ (mod \ n)$ 可以构造模多项式 :
$X$ 为模多项式 $f(x) = ((\Delta m + X)^e - c) \ mod \ N$ 的小整数解。
例题:这里由于没找到啥题目样例,索性自己随便出了一道,不考虑非预期解。
c = 49448440304854831648796534024125601382006282873198989997965557974794200333763817072355620545318651927253247674282578472637671741164408087215327482745901235293974786619481946963756529643023816474028709984009212852065178750039594108019217271743973042473197736068985706708503716012186147977316095727799381598075488417125
n = 28847074924932453349543409136399812128594610949367020026474778343570858319481313455200890189364023790182887175049408105958843453263073050626086662142940263874460213271683958427975341123423883215407111909499389249677340455477004237510991188529190235171007660645641687224704887400900068278836154730644879715422040757103147552875954913961588149167053461868101745063648215554184664115626793497487765708744642552805937987823454039925728887745567746569963466846339068171354494330823482202581747310450407677264654959638952096601645772638052521701110952634257302519671771900589919411338060623904602870338988690057676936333193
e = 3
m_high = ((m >> 88) << 88)
m_high = 0x666c61677b343833323734383733383438777975727975737238796538727938323372000000000000000000
题目分析,这里我们由代码 m_high = ((m >> 88) << 88) 可知,m的未知低位有 88 bits,根据上面的原理构造模多项式用 Coppersmith求解多项式的根即可恢复出明文 m。
sagemath实现 exp :
#sage
from gmpy2 import *
from Crypto.Util.number import *
c = 49448440304854831648796534024125601382006282873198989997965557974794200333763817072355620545318651927253247674282578472637671741164408087215327482745901235293974786619481946963756529643023816474028709984009212852065178750039594108019217271743973042473197736068985706708503716012186147977316095727799381598075488417125
n = 28847074924932453349543409136399812128594610949367020026474778343570858319481313455200890189364023790182887175049408105958843453263073050626086662142940263874460213271683958427975341123423883215407111909499389249677340455477004237510991188529190235171007660645641687224704887400900068278836154730644879715422040757103147552875954913961588149167053461868101745063648215554184664115626793497487765708744642552805937987823454039925728887745567746569963466846339068171354494330823482202581747310450407677264654959638952096601645772638052521701110952634257302519671771900589919411338060623904602870338988690057676936333193
e = 3
m_high = 0x666c61677b343833323734383733383438777975727975737238796538727938320000000000000000000000
kbits = 22*4
PR.<x> = PolynomialRing(Zmod(n))
f = (m_high + x)**e - c # 构造的模多项式
f = f.monic()
root = f.small_roots(X=2^kbits, beta=0.5) # 计算模多项式的小整数根
print(root)
m = (m_high + root[0])
print(long_to_bytes(int(m)))
enc = pow(m,3,n)
assert enc == c
print("ok")
运行结果:
[62194515593725596442703997]
b'flag{483274873848wyuryusr8ye8ry823r3r8327r8}'
ok
已知明文m的低位攻击
设明文 m 的二进制位表示为 :$mn ...m{k+1}m_k...p_1$ $(n>>k)$,其低位比特数据 $m_k ...m_1$ 被泄露。令 $\Delta m = m_k...m_1$ 为低位已知量, 设 $X = mn...m{k+1}$ 为高位未知量 ;由 $c \equiv m^e \ (mod \ n)$ 可以构造模多项式 :
$X$ 为模多项式 $f(x) = ((2^k*X + \Delta m)^e - c) \ mod \ N$ 的小整数解。(其中的 k 是 m 已知低位的比特数量)
例题 [2022天山固网杯]:
from Crypto.Util.number import *
from secret import flag
p = getPrime(512)
q = getPrime(512)
assert GCD(3, (p-1)*(q-1)) != 1
assert len(flag) == 40
assert flag.startswith(b'DASCTF{')
assert flag.endswith(b'}')
n = p*q
m = bytes_to_long(flag[7:-1]+b'12345678900987654321')
e = 3
c = pow(m, e, n)
print("n =", n)
print("m =", m&((1<<350)-1))
print("c =", c)
'''
n = 78143938921360185614860462235112355256968995028076215097413461371745388165946555700961349927305255136527151965763804585057604387898421720879593387223895933656350645970498558271551701970896688207206809537892771605339961799334047604053282371439410751334173463317244016213693285842193635136764938802757014669091
m = 1906077032611187208365446696459387107800629785754941498024021333398862239730761050657886407994645536780849
c = 50130000135496687335562420162077023127865865388254124043997590968769445787929013990729805222613912997653046528125102370938788632651827553831996692788561639714991297669155839231144254658035090111092408296896778962224040765239997700906745359526477039359317216610131441370663885646599680838617778727787254679678
'''
分析题目代码
assert len(flag) == 40
m = bytes_to_long(flag[7:-1]+b'12345678900987654321')
print("m =", m&((1<<350)-1))
从这三行代码可以知道:m 为 52 字节长度,1 byte = 8bit,所以 m 的值大约为 52*8 = 416 bits,现在 350 bits的低位数据已知,那么未知的高位数据大约为 :416 - 350 = 66 bits,所以我们在使用 Coppersmith 算法计算 X 时,设置根的界限也应该为 X=2^66
sagemath实现 exp :
#sage
from gmpy2 import *
from Crypto.Util.number import *
n = 78143938921360185614860462235112355256968995028076215097413461371745388165946555700961349927305255136527151965763804585057604387898421720879593387223895933656350645970498558271551701970896688207206809537892771605339961799334047604053282371439410751334173463317244016213693285842193635136764938802757014669091
m_low = 1906077032611187208365446696459387107800629785754941498024021333398862239730761050657886407994645536780849
c = 50130000135496687335562420162077023127865865388254124043997590968769445787929013990729805222613912997653046528125102370938788632651827553831996692788561639714991297669155839231144254658035090111092408296896778962224040765239997700906745359526477039359317216610131441370663885646599680838617778727787254679678
e = 3
PR.<x> = PolynomialRing(Zmod(n))
f = (x*2^350 + m_low)**e - c # 构造的模多项式
f = f.monic()
root = f.small_roots(X=2^66,beta=0.5)[0] # 计算模多项式的小整数根
print('root =',root)
m=root*2^350+m_low
print(long_to_bytes(int(m)))
这里我们设置 beta 参数使用默认值也是可以,因为根值数据量相对较小。
运行结果:
root = 15910343942542255508
b'739a9a9e50c9a8a5ba83ae2a8e75947012345678900987654321'
已知dq的低位攻击
这题属于结合了 dq泄露和依据题目信息构造一元多项式,然后用 Coppersmith 算法进行求解。也是一道很好的题目,供大家学习 Coppersmith 攻击利用。
例题:蓝帽杯2022 corrupted_key
注:只截取了和coppersmith相关的内容,不是完整的题目。目标是求解出私钥 p、q来。
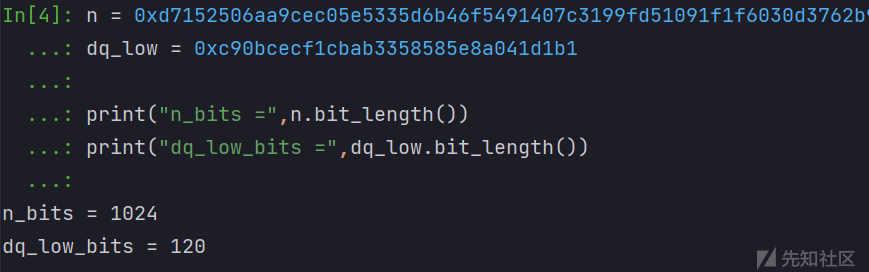
n = 0xd7152506aa9cec05e5335d6b46f5491407c3199fd51091f1f6030d3762b9e03f49c9dcdc075054e0cc148b974b41854bd93b4ee16a2a876ee62005e80ef806b7aa3b64b1bf9b1fa773e353d0cdb9ff9783ddd5f5e67499ad10f361e938d00b82a6a4c42a0535c5e76721798e86b45cd4b8d03b0d7e75c2be8766a1e843bdc641
e = 0x10001
dq_low = 0xc90bcecf1cbab3358585e8a041d1b1
qinvp = 0xe3016cb3609c1d643c167439c3b938b881f4237f24860d3b1cb85a626d5ccd4726964e0f8270d6c4df9ebfebcc538e4ee5e1a7b7368ede51ec6ae917f78eb598
分析题目:
先梳理已知条件和未知条件,已知条件: n,e,dq_low,qinvp
未知条件:d,p,q,dq
我们需要先求出 dq,然后通过 dq泄露的原理求出 q,然后用 qinvp 的公式构造一元多项式,结合 coppersmith算法求多项式的根
(其中:dq = d % (q-1),qinvp = q^(-1) % p ,qinvp为模数p下q的逆元素)
构造一元多项式的过程如下:
和 dq 泄露的原理一样,由:
$ed \equiv 1 \ mod \ (q-1)(p-1) \Rightarrow ed = 1+k_1(q-1)(p-1)$
$dq \equiv d \ mod \ (q-1) \Rightarrow edq \equiv ed \ mod \ (q-1)$
将上面两式相结合得到:
$edq = (1+k_1(q-1)(p-1)) \ mod \ (q-1) \Rightarrow e*dq = 1 \ mod \ (q-1)$
$edq = 1 + k_1(q-1) \Rightarrow (e*dq - 1)/k_1 + 1 = q$
又由 $qinvp \equiv q^{-1} \ mod \ p \Rightarrow qinvpq \equiv1 \ mod \ p \Rightarrow qinvpq = 1 + k_2p \Rightarrow qinvpq^2 - q = k_2n \Rightarrow qinvpq^2 - q \equiv 0 \ mod \ n$
将上面的关于q 的等式带入,得到:
$qinvp ((edq - 1)/k_1 + 1)^2 - ( (e*dq - 1)/k_1 + 1) \equiv 0 \ mod \ n$
等式1:令 qinvp 为 t,化简得到:$t (edq-1)^2 + k_1(2t-1)(edq-1) + k_1^2*(t-1) \equiv 0 \ mod \ n$
等式2:因为已知 dq 的低比特位数据量为120bits,我们令: $dq = (2^{120}*x + dqlow)$
关于变量 k1 ,由 $edq = 1 + k_1(q-1)$ 可知:dq < q - 1 ,所以 $0 < k_1 < e$ ,确定 k1 的范围可以爆破 k1 找到符合解的值。
其他变量都已知,将等式1、2相结合,构造成模多项式然后用 coppersmith求解小整数根 x 即可恢复出 dq,然后再用上面推导的公式 $(e*dq - 1)/k_1 + 1 = q$ 得到 q 的值。
sagemath实现 exp :
#sage
from gmpy2 import *
from tqdm import tqdm
from sage.all import *
n = 0xd7152506aa9cec05e5335d6b46f5491407c3199fd51091f1f6030d3762b9e03f49c9dcdc075054e0cc148b974b41854bd93b4ee16a2a876ee62005e80ef806b7aa3b64b1bf9b1fa773e353d0cdb9ff9783ddd5f5e67499ad10f361e938d00b82a6a4c42a0535c5e76721798e86b45cd4b8d03b0d7e75c2be8766a1e843bdc641
e = 0x10001
dq_low = 0xc90bcecf1cbab3358585e8a041d1b1
qinvp = 0xe3016cb3609c1d643c167439c3b938b881f4237f24860d3b1cb85a626d5ccd4726964e0f8270d6c4df9ebfebcc538e4ee5e1a7b7368ede51ec6ae917f78eb598
t = qinvp
PR.<x> = PolynomialRing(Zmod(n))
dq = (2^120*x + dq_low)
kbit = 512 - 120 # 用于设置根X的界限
for k in tqdm(range(e,1,-1)):
f = t*pow(e*dq - 1,2) + k*(2*t-1)*(e*dq - 1) + pow(k,2)*(t-1) # 构造的模多项式
f = f.monic()
root = f.small_roots(X=2^kbit,beta=0.5) # 计算模多项式的小整数根
if root:
dq = 2^120*root[0] + dq_low
print('k =',k)
q = int((e*dq - 1)//k + 1)
p = n//q
if p*q == n:
print('dq =',dq)
print('p =',p)
print('q =',q)
break
运算结果:

-
-
-
-
-
-
-

 转载
转载
 分享
分享

感谢分享,但是文章中的公式没显示出来耶,影响阅读体验
感谢分享,有没有打算出格密码相关的内容