RSA系列之基础实战 1

导入

从这个系列开始，我将从简单到困难的将RSA中的题型不断更新加入此，无论是典型的dp泄露为代表计算为主的题型，或是以按行加密的代码理解为主的题型，笔者将尽力整理成册，并辅以自己的理解和总结。希望能帮助到各位读者，若有笔误或其余错误，敬请谅解并联系我更改，共勉。

基础知识回顾

（注：熟悉该内容可跳过）

φ(n):欧拉函数,小于等于n的正整数中与n互质的数的总数
      1.如果n是质数的某一个次方，即 n = p^k (p为质数，k为大于等于1的整数)，则
         φ(p^k) = p^k - p^(k-1)
     2.如果n可以分解成两个互质的整数之积，n = p1 × p2
       则φ(n) = φ(p1p2) = φ(p1)φ(p2)
     3.欧拉定理：如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立:
         a^φ(n)= 1 ( mod n)
       欧拉定理：如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：
         a^φ(n) ≡ 1 ( mod n)
     4.模反元素：如果两个正整数a和n互质，那么一定可以找到整数b，ab被n除的余数是1
     ab===1(mod n),b叫做a的模反元素

RSA加密过程
p:质数q  q:质数q  n:质数n=p*q
φ(n)=φ(p*q)=φ(p)φ(q)=(p-1)*(q-1)
e:随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质
d:e对于φ(n)的模反元素d 即：ed ≡ 1 (mod φ(n))
(n,e):公钥  (n,d):私钥
m:明文  c:用公钥加密后的密文
     那么，有无可能在已知n和e的情况下，推导出d？
     　　（1）ed≡1 (mod φ(n))。只有知道e和φ(n)，才能算出d。
     　　（2）φ(n)=(p-1)(q-1)。只有知道p和q，才能算出φ(n)。
     　　（3）n=pq。只有将n因数分解，才能算出p和q。
     结论：如果n可以被因数分解，d就可以算出，也就意味着私钥被破解

    加密要用公钥(n,e)，m已知m*e ≡ c (mod n) 
    加密算出c，加 密 公 式 ： m*e ≡ c ( mod n ) → c = m*e – k*n
    解密要用私钥(n,d)，解密公式：cd ≡ m (mod n)

例题

1.最最基础的RSA

题目描述：

N = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085
import hashlib
flag = "flag{" + hashlib.md5(hex(d)).hexdigest() + "}"

题目分析：

由flag可知要求出d
又ed≡1 (mod φ(n))，而φ(n)=(p-1)(q-1)。只有知道p和q，才能算出φ(n)
由N 可通过分解n,得p,q的网站得到p与q
之后通过d = gmpy2.invert(e,phi)得到d
解d脚本：

import gmpy2
N = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085
p = 9046853915223503351787031888977627106934564043204783593118678181991596316582877057556463152579621699010610569526573031954779520781448550677767565207407183
q = 11273732364123571293429600400343309403733952146912318879993851141423284675797325272321856863528776914709992821287788339848962916204774010644058033316303937
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
print(d)

但为什么解出d后仍得不到flag？？？

【字符串必须在哈希之前进行编码】

所以完整且正确的代码如下：

import gmpy2
import hashlib
N = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085
p = 9046853915223503351787031888977627106934564043204783593118678181991596316582877057556463152579621699010610569526573031954779520781448550677767565207407183
q = 11273732364123571293429600400343309403733952146912318879993851141423284675797325272321856863528776914709992821287788339848962916204774010644058033316303937
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
flag = "flag{" + hashlib.md5(hex(d).encode()).hexdigest() + "}"
print(flag)
# flag{8159e6c4abdd3b94ce461ed9a1a24017}

2.dp

题目描述：

e = 65537
n = 156808343598578774957375696815188980682166740609302831099696492068246337198792510898818496239166339015207305102101431634283168544492984586566799996471150252382144148257236707247267506165670877506370253127695314163987084076462560095456635833650720606337852199362362120808707925913897956527780930423574343287847
c = 108542078809057774666748066235473292495343753790443966020636060807418393737258696352569345621488958094856305865603100885838672591764072157183336139243588435583104423268921439473113244493821692560960443688048994557463526099985303667243623711454841573922233051289561865599722004107134302070301237345400354257869
dp = 734763139918837027274765680404546851353356952885439663987181004382601658386317353877499122276686150509151221546249750373865024485652349719427182780275825

题目分析：

c = m^e mod n
m = c^d mod n
ϕ(n)=(p−1)*(q−1)
d∗e ≡ 1 mod ϕ(n)
dp = d mod (p−1)

由上式可以得到

dp*e≡d*e mod (p−1)

因此可以得到

式1：d∗e=k∗(p−1)+dp∗e
式2：d∗e≡1 mod ϕ(n)

式1带入式2

=> k1∗(p−1)+dp∗e ≡1 mod ϕ(n)

=> k1∗(p−1)+dp∗e ≡1 mod (p−1)∗(q−1)

=> k1∗(p−1)+dp∗e = k2*(p−1)∗(q−1)+1

=> dp*e = k2*(p−1)∗(q−1)+1-k1∗(p−1)

=> dp*e = (p-1)*[k2*(q-1)-k1]+1

因dp<p−1（dp是d//（p-1）的取整，dp<p−1）

所以e > k2∗(q−1)−k1

再次回到

dp e = (p-1)[k2*(q-1)-k1]+1

假设 x=k2∗(q−1)−k1

那么x的范围为 (0,e)

x∗(p−1)+1=dp∗e

枚举 x 求出p-1，即遍历(0,e)的范围，其中肯定有一个p可以被n整除，那么求出p和q

最终运行代码得到 flag{dp_leaking_1s_very_d@angerous} (嚯！原来题目就是答案啊！)
首先我们先看下解题脚本，再进行分析：

e = 65537
n = 156808343598578774957375696815188980682166740609302831099696492068246337198792510898818496239166339015207305102101431634283168544492984586566799996471150252382144148257236707247267506165670877506370253127695314163987084076462560095456635833650720606337852199362362120808707925913897956527780930423574343287847
c = 108542078809057774666748066235473292495343753790443966020636060807418393737258696352569345621488958094856305865603100885838672591764072157183336139243588435583104423268921439473113244493821692560960443688048994557463526099985303667243623711454841573922233051289561865599722004107134302070301237345400354257869
dp = 734763139918837027274765680404546851353356952885439663987181004382601658386317353877499122276686150509151221546249750373865024485652349719427182780275825
for i in range(1,65535):
    p = (dp*e-1)//i+1
    if n%p == 0:
        q = n//p
        break
# print(p)
# print(q)
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
flag = libnum.n2s(int(m)).decode()
print(flag)

主要还是这串代码--->

for i in range(1,65535):
    p = (dp*e-1)//i+1
    if n%p == 0:
        q = n//p
        break

3.ROLL按行加密

题目描述：

{920139713,19}

704796792
752211152
274704164
18414022
368270835
483295235
263072905
459788476
483295235
459788476
663551792
475206804
459788476
428313374
475206804
459788476
425392137
704796792
458265677
341524652
483295235
534149509
425392137
428313374
425392137
341524652
458265677
263072905
483295235
828509797
341524652
425392137
475206804
428313374
483295235
475206804
459788476
306220148

题目分析：

说实话一开始没看懂题目的意思，看完别人的wp才知道括号里面的两个数字是 n 与 e ,后面的是拆分的密文 c ,原来题目中的 roll 是利用题中多个 c 滚动拼接 flag 的意思
以下是解题代码：

import libnum
import gmpy2
list1 = [704796792,
752211152,
274704164,
18414022,
368270835,
483295235,
263072905,
459788476,
483295235,
459788476,
663551792,
475206804,
459788476,
428313374,
475206804,
459788476,
425392137,
704796792,
458265677,
341524652,
483295235,
534149509,
425392137,
428313374,
425392137,
341524652,
458265677,
263072905,
483295235,
828509797,
341524652,
425392137,
475206804,
428313374,
483295235,
475206804,
459788476,
306220148]
flag = ''
n = 920139713
e = 19
p = 18443
q = 49891
phi = (p-1)*(q-1)
for i in list1:
    c = i
    d = libnum.invmod(e,phi)
    m = pow(c,d,n)
    # string = libnum.n2s(m) 此两句的作用等同于 flag += chr(m)
    # flag += string.decode()
    flag += chr(m)
print(flag)

收获与体会：

又了解了一种 rsa 题型 ---> 滚动拼接法求 flag
懂了 str.decode() 的意思，即

string = libnum.n2s(m)
flag += string.decode()
此两句的作用等同于
flag += chr(m)

4.古典1

题目描述：

题目分析：

翻译一下可知：

前提：用0、1、2、…..枚举字母表25
使用RSA系统
加密：0156 0821 1616 0041 0140 2130 1616 0793
公钥：2537和13
私钥：2537和937

从提示可以得知 n = 2537 , e = 13 , d = 937
分解 n ,可知 p = 43 , q = 59
做过 buu RSAROLL 1 便可知道此题大致考的什么
里面的 “ 0156 0821 1616 0041 0140 2130 1616 0793 ” 即是 c ,只不过是多个 c ,将解出来的明文拼接在一起便可得到 flag
代码如下：

a = 'abcdefghigklmnopqrstuvwxyz'
p = 43
q = 59
e = 13
d = 937
c = '0156 0821 1616 0041 0140 2130 1616 0793'.split(' ')
flag = ''
n = p*q
for i in c:
    flag += a[pow(int(i),d,n)]
print(flag)
#flag{iloveyou}

收获与体会：

此题有一个特殊之处，即里面的 c , e , n 都很小，很反常！
如果按 buu RSAROLL 这道题来写的话，得不到答案，因为打印 pow(int(i),d,n) 后会得到

8
11
14
21
4
24
14
20

一串很小的数字，对应ascii码后会得到一些特别的东西，没有字母也没有数字

所以就会想到可能是按照26个字母表进行转换，位置一一对应即可转化成功得到 flag
所以数字在1~26之间就转字母便，大于26就转 ascii 码

5.共享素数+爆破

题目描述：

import gmpy2
from Crypto.Util.number import getPrime,bytes_to_long

flag=open("flag","rb").read()

p=getPrime(1024)
q=getPrime(1024)
assert(e<100000)
n=p*q
m=bytes_to_long(flag)
c=pow(m,e,n)
print c,n
print pow(294,e,n)

p=getPrime(1024)
n=p*q
m=bytes_to_long("BJD"*32)
c=pow(m,e,n)
print c,n

c1 = 12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120
n1 = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
_294c = 381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
c2 = 979153370552535153498477459720877329811204688208387543826122582132404214848454954722487086658061408795223805022202997613522014736983452121073860054851302343517756732701026667062765906277626879215457936330799698812755973057557620930172778859116538571207100424990838508255127616637334499680058645411786925302368790414768248611809358160197554369255458675450109457987698749584630551177577492043403656419968285163536823819817573531356497236154342689914525321673807925458651854768512396355389740863270148775362744448115581639629326362342160548500035000156097215446881251055505465713854173913142040976382500435185442521721  
n2 = 12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047

题目分析：

从题目中知道e<100000,比较小，且有多个n与c，且多个n共用一个q,所以想到共享素数,如此便可求到q,然后得到p
之后d也容易得到，最后只剩e不知道啦，然而题目中表示e较小，直接爆破求出，几个未知数都知道了，那flag岂不手到擒来啦！
以下是解题代码：

c1 = 12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120
n1 = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
_294c = 381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
c2 = 979153370552535153498477459720877329811204688208387543826122582132404214848454954722487086658061408795223805022202997613522014736983452121073860054851302343517756732701026667062765906277626879215457936330799698812755973057557620930172778859116538571207100424990838508255127616637334499680058645411786925302368790414768248611809358160197554369255458675450109457987698749584630551177577492043403656419968285163536823819817573531356497236154342689914525321673807925458651854768512396355389740863270148775362744448115581639629326362342160548500035000156097215446881251055505465713854173913142040976382500435185442521721  
n2 = 12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047

import gmpy2
import libnum
# n1和 n2公用了一个 q 用gcd欧几里得算法求得q
p = gmpy2.gcd(n1,n2)
q = n1//p
print(p)
phi = (q-1)*(p-1)
# 此时知道e即可解题 因为我们知道pow(294,e,n) 还知道e的范围所以可以爆破e
for i in range(100000):
    if pow(294,i,n1) == _294c:
        e = i
        break

d = gmpy2.invert(e,phi)
m = pow(c1,d,n1)
print(libnum.n2s(int(m)))
# b'BJD{p_is_common_divisor}'

6.位数之谜

题目描述：

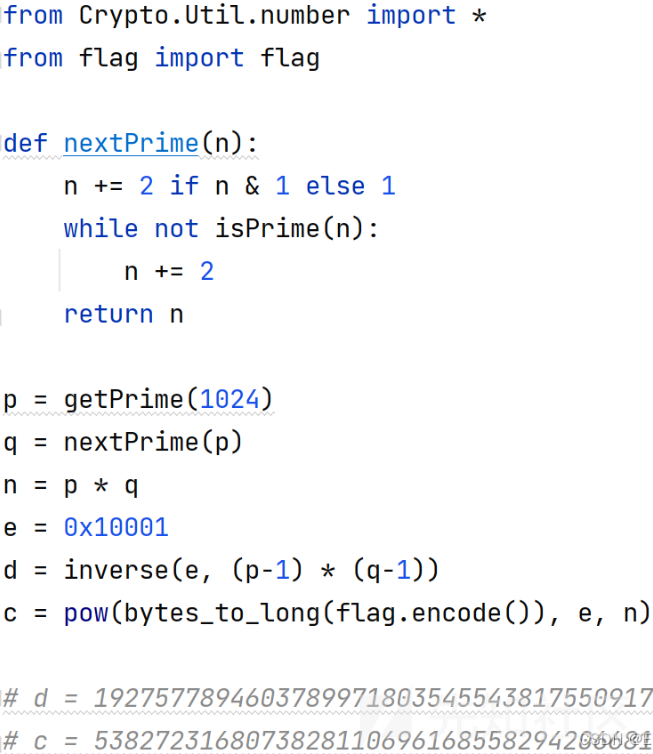
题目分析：

首先明确两个公式：

e*d = 1 mod (p-1)(q-1)
ed1 = e*d - 1 = k(p-1)(q-1)

想要解出此题，我们必须知道n,而要知道n,我们要知道p和q的值
通过 e*d 的计算，我们知道其长度为2064位，而生成p的条件为 getPrime(1024)，所以（p-1)（q-1）应该为2048位

此处所说的位数长度是以Bit为单位，加一减一都不影响位数，相乘的话即为位数相加，这些性质记住就好，以下是计算代码：

from Crypto.Util.number import *
e = 65537 # 转二进 e = 0b10000000000000001,直接数得到长度为17
d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
print(gmpy2.bit_length(e*d))
# 2064
p = getPrime(1024)
print(gmpy2.bit_length(p))
# 1024
print(gmpy2.bit_length(p-1))
# 1024

又 ed1 = e*d - 1 = k(p-1)(q-1)，2064-2048 = 16，所以k值必在 pow(2,15)至pow(2,16)之间（想知道为什么看结尾的知识总结，此处专注解题，不深层探究）
所以，我们可以利用此条件暴力求解k值，从而求出(p-1)*(q-1),间接求出 p 和 q 的值
那如何间接法呢？
首先我们求得了(p-1)(q-1),而p和q是两个相邻的质数，所以我们可以使用sympy库对p,q进行求解。思路为先对(p-1)(q-1)开方，再求得大于开方所得数和小于开方所得数的质数

p = sympy.prevprime(gmpy2.iroot((e*d-1)//i,2)[0])
q = sympy.nextprime(p)

其中 sympy.prevprime(x)是求小于x最近的质数，sympy.nextprime(x)是求大于x最近的质数。
解题代码如下：

import gmpy2
from Crypto.Util.number import long_to_bytes
import sympy
# e = 0x10001
e = 65537
d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
c = 5382723168073828110696168558294206681757991149022777821127563301413483223874527233300721180839298617076705685041174247415826157096583055069337393987892262764211225227035880754417457056723909135525244957935906902665679777101130111392780237502928656225705262431431953003520093932924375902111280077255205118217436744112064069429678632923259898627997145803892753989255615273140300021040654505901442787810653626524305706316663169341797205752938755590056568986738227803487467274114398257187962140796551136220532809687606867385639367743705527511680719955380746377631156468689844150878381460560990755652899449340045313521804
p = 0
q = 0

for k in range(pow(2,15),pow(2,16)):
    #  pow(x,y) ---> x 的 y 次方
    #  pow(x,y,z) ---> x 的 y 次方后，取余 z
    if (e*d-1)%k == 0:
        p = sympy.prevprime(gmpy2.iroot((e*d-1)//k,2)[0])
        # sympy.prevprime(x)是求大于x最近的质数
        # iroot(x,n) ---> x开n次根 ,返回值有两个，前一个是开方出来的整数部分，后一个是能否开出来，若能则为true,不能则为flase
        q = sympy.nextprime(p)
        # sympy.nextprime(x)是求小于x最近的质数
        if (p-1)*(q-1) == (e*d-1)//k:
            break

n = p*q
m = pow(c,d,n)
m1 = long_to_bytes(m)
print(m1)
#flag{70u2_nn47h_14_v3ry_gOO0000000d}

收获与体会：

了解了一些字节的相关知识
知道了函数 sympy.prevprime(x)和sympy.nextprime(x)的相关知识

sympy.prevprime(x)是求小于x最近的质数
sympy.nextprime(x)是求大于x最近的质数

回顾了iroot(x,n) 和 pow(x,y) 的相关知识

iroot(x,n) ---> x开n次根,返回值有两个，前一个是开方出来的整数部分，后一个是能否开出来，若能则为true,不能则为flase
pow(x,y) ---> x 的 y 次方
pow(x,y,z) ---> x 的 y 次方后，取余 z

7.威尔逊

题目描述：

import sympy
import random

def myGetPrime():
    A= getPrime(513)
    print(A)
    B=A-random.randint(1e3,1e5)
    print(B)
    return sympy.nextPrime((B!)%A)
p=myGetPrime()
#A1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467234407
#B1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467140596

q=myGetPrime()
#A2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858418927
#B2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858351026

r=myGetPrime()

n=p*q*r
#n=85492663786275292159831603391083876175149354309327673008716627650718160585639723100793347534649628330416631255660901307533909900431413447524262332232659153047067908693481947121069070451562822417357656432171870951184673132554213690123308042697361969986360375060954702920656364144154145812838558365334172935931441424096270206140691814662318562696925767991937369782627908408239087358033165410020690152067715711112732252038588432896758405898709010342467882264362733
c=pow(flag,e,n)
#e=0x1001
#c=75700883021669577739329316795450706204502635802310731477156998834710820770245219468703245302009998932067080383977560299708060476222089630209972629755965140317526034680452483360917378812244365884527186056341888615564335560765053550155758362271622330017433403027261127561225585912484777829588501213961110690451987625502701331485141639684356427316905122995759825241133872734362716041819819948645662803292418802204430874521342108413623635150475963121220095236776428
#so,what is the flag?

题目分析：

首先我们先看到 n = p q r （n 分解成了三个素数） ,而 e,c 都知道，所以要求明文 m = pow(c,d,n) 先要求出 d 来
而 d = gmpy2.invert(e,phi)
其中欧拉函数 phi = (p-1) (q-1) (r-1)
所以要求 d ,那么要求出 p 与 q
代码中 p = myGetPrime() = sympy.nextPrime((B!)%A)

sympy.nextprime(x) 是求大于x最近的质数

所以最终要求 (B!)%A，即B的阶乘模A，其中 A,B 都知道，那么B!（B的阶乘）怎么求呢？
有一个定理可以解决这个问题，即威尔逊定理

威尔逊定理

当且仅当p为素数时：( p -1 ) ! ≡ -1 ( mod p ) ---> (p-1) ! +1=0 (mod p)

A = getPrime(513)，可知A为素数，又 B=A-random.randint(1e3,1e5)，通过威尔逊定理，可知(A-1) ! +1≡0 (mod A)，故B!(B+1)(B+2)…(A-1) ≡ -1 (mod A)，即B! * C = ≡ -1 ( mod A )，其中C = (A - 1)! / (B) !，也就是B之后的数字之积
两边同时乘上C的逆元C1*(C * C1 = 1)，B ! = -1 * C1(mod A1)
B ! 求出来了，那么 p = myGetPrime() = sympy.nextPrime((B!)%A) 也就求出来了
如此，p,q 都求出来了，r = n // (p * q) ,自此p,q,r,都求出来了，最终flag也就出来了
代码如下：

import libnum
import sympy
import gmpy2

A1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467234407
B1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467140596
A2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858418927
B2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858351026
n=85492663786275292159831603391083876175149354309327673008716627650718160585639723100793347534649628330416631255660901307533909900431413447524262332232659153047067908693481947121069070451562822417357656432171870951184673132554213690123308042697361969986360375060954702920656364144154145812838558365334172935931441424096270206140691814662318562696925767991937369782627908408239087358033165410020690152067715711112732252038588432896758405898709010342467882264362733
# e=0x1001，转十进制
e = 4097
c=75700883021669577739329316795450706204502635802310731477156998834710820770245219468703245302009998932067080383977560299708060476222089630209972629755965140317526034680452483360917378812244365884527186056341888615564335560765053550155758362271622330017433403027261127561225585912484777829588501213961110690451987625502701331485141639684356427316905122995759825241133872734362716041819819948645662803292418802204430874521342108413623635150475963121220095236776428
def mydecryp(A,B):
    C1 = 1
    temp = pow(-1,1,A) # temp=-1 mod A
    for i in range(B+1,A):
        C1 = (C1*gmpy2.invert(i,A))%A # C1是从B+1~A中每个数对A的逆元的乘积
    return sympy.nextprime((C1*temp)%A) # (C1*temp) = B!， (C1*temp)%A = (B!)%A

p = mydecryp(A1,B1)
q = mydecryp(A2,B2)
r = n//p//q
phi = (p-1)*(q-1)*(r-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(libnum.n2s(int(m)))
#flag{wm-CongrAtu1ation4-1t4-ju4t-A-bAby-R4A}

8.方程计算

题目描述：

A=(((y%x)**5)%(x%y))**2019+y**316+(y+1)/x
p=next_prime(z*x*y)
q=next_prime(z)
A =  2683349182678714524247469512793476009861014781004924905484127480308161377768192868061561886577048646432382128960881487463427414176114486885830693959404989743229103516924432512724195654425703453612710310587164417035878308390676612592848750287387318129424195208623440294647817367740878211949147526287091298307480502897462279102572556822231669438279317474828479089719046386411971105448723910594710418093977044179949800373224354729179833393219827789389078869290217569511230868967647963089430594258815146362187250855166897553056073744582946148472068334167445499314471518357535261186318756327890016183228412253724
n =  117930806043507374325982291823027285148807239117987369609583515353889814856088099671454394340816761242974462268435911765045576377767711593100416932019831889059333166946263184861287975722954992219766493089630810876984781113645362450398009234556085330943125568377741065242183073882558834603430862598066786475299918395341014877416901185392905676043795425126968745185649565106322336954427505104906770493155723995382318346714944184577894150229037758434597242564815299174950147754426950251419204917376517360505024549691723683358170823416757973059354784142601436519500811159036795034676360028928301979780528294114933347127
c =  41971850275428383625653350824107291609587853887037624239544762751558838294718672159979929266922528917912189124713273673948051464226519605803745171340724343705832198554680196798623263806617998072496026019940476324971696928551159371970207365741517064295956376809297272541800647747885170905737868568000101029143923792003486793278197051326716680212726111099439262589341050943913401067673851885114314709706016622157285023272496793595281054074260451116213815934843317894898883215362289599366101018081513215120728297131352439066930452281829446586562062242527329672575620261776042653626411730955819001674118193293313612128

题目分析：

这题看了别人写的题解，知道了两种不同的解题方法
第一种是契合题目所给字母，先通过爆破求出x,y，但奇怪的是我用pycharm重写了一遍他们的代码，都出现了报错：
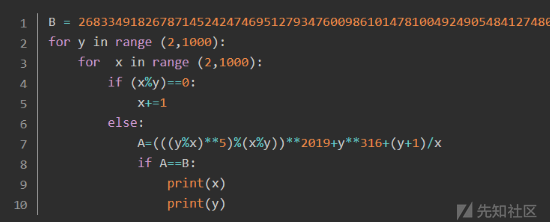
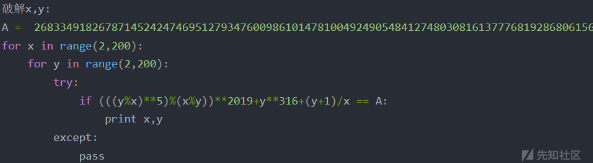
上面两种一个是报错，一个是直接结束程序，反正都求不出x,y（我也求不出）
所以尝试了另外一种方法：直接爆破求e,（p,q可以通过n分解得到），所以字母都求出来了，那么最后答案也就差不多了，代码如下：

from Crypto.Util.number import *
A = 2683349182678714524247469512793476009861014781004924905484127480308161377768192868061561886577048646432382128960881487463427414176114486885830693959404989743229103516924432512724195654425703453612710310587164417035878308390676612592848750287387318129424195208623440294647817367740878211949147526287091298307480502897462279102572556822231669438279317474828479089719046386411971105448723910594710418093977044179949800373224354729179833393219827789389078869290217569511230868967647963089430594258815146362187250855166897553056073744582946148472068334167445499314471518357535261186318756327890016183228412253724
n = 117930806043507374325982291823027285148807239117987369609583515353889814856088099671454394340816761242974462268435911765045576377767711593100416932019831889059333166946263184861287975722954992219766493089630810876984781113645362450398009234556085330943125568377741065242183073882558834603430862598066786475299918395341014877416901185392905676043795425126968745185649565106322336954427505104906770493155723995382318346714944184577894150229037758434597242564815299174950147754426950251419204917376517360505024549691723683358170823416757973059354784142601436519500811159036795034676360028928301979780528294114933347127
c = 41971850275428383625653350824107291609587853887037624239544762751558838294718672159979929266922528917912189124713273673948051464226519605803745171340724343705832198554680196798623263806617998072496026019940476324971696928551159371970207365741517064295956376809297272541800647747885170905737868568000101029143923792003486793278197051326716680212726111099439262589341050943913401067673851885114314709706016622157285023272496793595281054074260451116213815934843317894898883215362289599366101018081513215120728297131352439066930452281829446586562062242527329672575620261776042653626411730955819001674118193293313612128
p = 842868045681390934539739959201847552284980179958879667933078453950968566151662147267006293571765463137270594151138695778986165111380428806545593588078365331313084230014618714412959584843421586674162688321942889369912392031882620994944241987153078156389470370195514285850736541078623854327959382156753458569
q = 139916095583110895133596833227506693679306709873174024876891023355860781981175916446323044732913066880786918629089023499311703408489151181886568535621008644997971982182426706592551291084007983387911006261442519635405457077292515085160744169867410973960652081452455371451222265819051559818441257438021073941183

for i in range(2,100000): # 此时的i即为e
    if isPrime(i): # 判断i是否为素数
        try:
            d = gmpy2.invert(i,(p-1)*(q-1))
            m = pow(c,d,n)
            flag = libnum.n2s(int(m)) # 此时 type(flag) = <class 'bytes'>,所以下面要转字符串，一开始没转字符串报错，所以才会想到这里
            if 'CTF' in str(flag) or 'flag' in str(flag):
                print(flag,'\n',i)
        except ZeroDivisionError:
            continue
            #flag{wm-l1l1ll1l1l1l111ll}，e = 65537

收获与体会:

真是巧了，e = 65537
所以如果以后要求e来求flag的，我们可以先大胆令e = 65537来试一下，没准就瞎猫碰上死耗子，答案就出来了，省时还省力（但遇上这种题的可能性确实挺小的）

知识总结：

1.

当出现多个c（并没有多个n）则想到拼接法。若每个c相对偏小，那么就意味着求出的m相对偏小，若m <= 26 则想到对应26个字母表，若m > 26，则直接 flag += chr(m)

2.

sympy.prevprime(x)是求小于x最近的质数
sympy.nextprime(x)是求大于x最近的质数

3.

encode(),decode()相关小知识

encode() 方法以指定的编码格式编码字符串，默认编码为 ‘utf-8’。

对应的解码方法：bytes decode() 方法，bytes:字节。该方法返回编码后的字符串，它是一个 bytes 对象实例

bytes通过decode（）转换为str（字符串）

str通过encode（）转换为bytes（二进制）

在python3中，encode（）和decode（）默认使用UTF-8

print('你好'.encode('utf-8'))
# b'\xe4\xbd\xa0\xe5\xa5\xbd' (转为二进制形式)

print(b'\xe4\xbd\xa0\xe5\xa5\xbd'.decode())
# 你好 (转为字符串形式)

print('passport'.encode('utf-8'))
# b'passport'

print(b'passport'.decode())
# passport

4.

b2a_hex(data)，a2b_hex(hexstr)，hexlify(data)，unhexlify(hexstr) 相关知识

b2a_hex(data) = hexlify(data)：
返回二进制数据的十六进制表示。每个字节被转换成相应的2位十六进制表示形式。因此，得到的字符串是是原数据长度的两倍。
a2b_hex(hexstr) = unhexlify(hexstr)：
从十六进制字符串hexstr返回二进制数据。是b2a_hex的逆向操作。 hexstr必须包含偶数个十六进制数字（可以是大写或小写），否则报TypeError。
例如：

b = binascii.b2a_hex('woker'.encode()) # 0x4244 2进制数据转16进制  
c = binascii.a2b_hex('0x4244'.encode()) # woker 16进制转二进制数据

5.

当出现多个c（并没有多个n）则想到拼接法。若每个c相对偏小，那么就意味着求出的m相对偏小，则直接 flag += chr(m)

6.

出现多个n与c，若e很小（小于100），则考虑低加密指数攻击，若e相对较小（小于100000）则可想到n之间不互素的情况