什么是随机

在通常的说法中，随机性是指事件中明显实际缺乏可预测性。事件、符号或步骤通常没有顺序

举个例子，比如我们在抛硬币，硬币的结果取决于很多因素，比如说我们施加的力，空气阻力，引力等，但是如果我们知道影响硬币的所有因素，并且知道这些因素准确的值，我们就能预测硬币落下时，是正面还是反面

伪随机

假如我们有一个算法，我们给他设置一个初始值，然后用这个算法生成下一个数字，然后再用生成的这个数字继续生成下一个……

12 --------> 30 --------> 57 --------> 33

这个初始值被称之为seed（种子），过段时间后我们可以得到一组相同的数字，这个过程叫做周期，周期越大，说明我们的算法越好，这种随机数生成的算法被称之为伪随机，它不是真正的随机生成

伪随机生成器通常用于游戏中，比如角色一开始生成的地方，但是不会用于密码学中，因为在一定条件下，伪随机生成器是可以被破解的

Math.random

在JavaScript中，有一个叫Math.random随机生成的函数，他是一个原生的函数，几乎所有的JavaScript框架都包含这个函数

https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Math/random

Math.random函数会返回一个大于0且小于1的浮点伪随机数，chrome浏览器也用的是JavaScript，并且包含了这个函数，使用的引擎是v8
而v8是开源的，并且是由google进行维护的

https://github.com/v8/v8/tree/7a4a6cc6a85650ee91344d0dbd2c53a8fa8dce04

https://v8.dev/blog/math-random

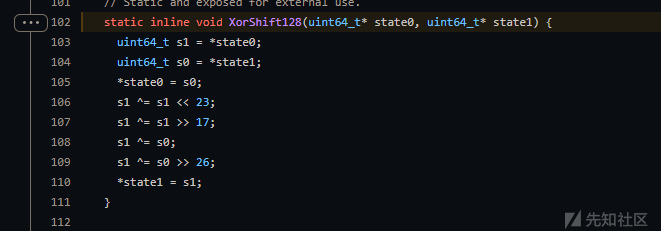
在官方的GitHub上有一个xorshift128+的算法，现在来分析math.random函数的源代码

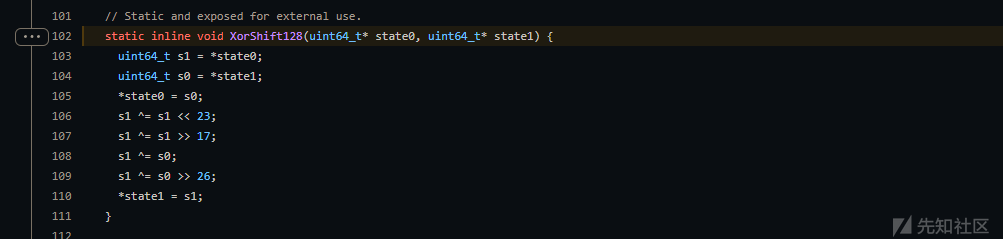
static inline void XorShift128(uint64_t* state0, uint64_t* state1) {
    uint64_t s1 = *state0;
    uint64_t s0 = *state1;
    *state0 = s0;
    s1 ^= s1 << 23;
    s1 ^= s1 >> 17;
    s1 ^= s0;
    s1 ^= s0 >> 26;
    *state1 = s1;
  }

看起来并不复杂，只是一些异或操作和移位的操作，这个函数将state0和state1变成s0和s1，然后s1进行了异或和移位
可以用z3这个smt求解器去破解它

z3

z3是由微软公司开发的smt求解器，我们可以将问题作为方程式列出，然后指定约束，z3就可以自动的解决这个问题

比如下面这个方程式

x + 2y = 7

可以使用z3来帮助我们计算x和y的值

from z3 import *

x = Int('x')
y = Int('y')
solve(x + 2*y == 7)

对Math.random函数破解

首先，用z3创建64位的占位符值，因为xorshift128有两个状态，所以将这两个状态设置为占位符变量

solver = z3.Solver()
se_state0, se_state1 = z3.BitVecs("se_state0 se_state1", 64)

然后还需要从v8生成的随机值进行运算，按下f12，进入控制台，输入以下代码，随机生成五个数

Array.from(Array(5), Math.random)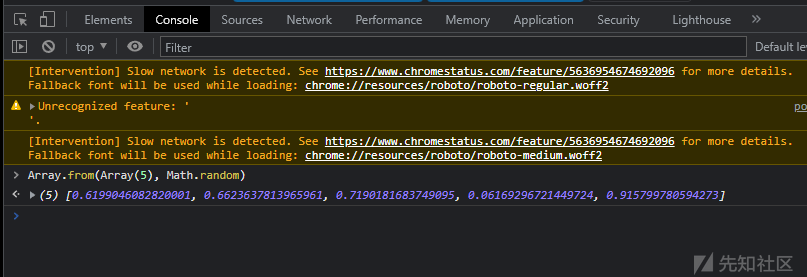

把这五个数放到脚本里，遍历这五个随机数

sequence = [0.6199046082820001, 0.6623637813965961, 0.7190181683749095, 0.06169296721449724, 0.915799780594273]
sequence = sequence[::-1]

然后直接将v8 xorshift128算法的源代码复制过来，做一些改动

for i in range(len(sequence)):
    se_s1 = se_state0   #用占位符值替换状态
    se_s0 = se_state1   #用占位符值替换状态
    se_state0 = se_s0   
    se_s1 ^= se_s1 << 23
    se_s1 ^= z3.LShR(se_s1, 17)  #设置逻辑移位而不是算数移位
    se_s1 ^= se_s0
    se_s1 ^= z3.LShR(se_s0, 26)
    se_state1 = se_s1

然后还需要写一些代码来进行运算

float_64 = struct.pack("d", sequence[i] + 1) #然后获取 se_state0的值并用struct模块把它变成双精度的值
    u_long_long_64 = struct.unpack("<Q", float_64)[0] #将其解压位64位无符号的整数
    mantissa = u_long_long_64 & ((1 << 52) - 1) #得到尾数的低52位再减去1
    solver.add(int(mantissa) == z3.LShR(se_state0, 12)) #添加约束来比较尾数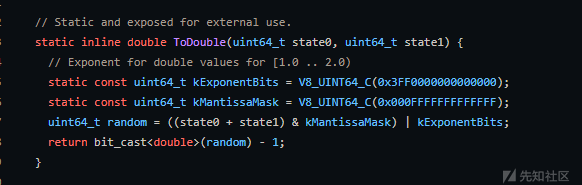

state0 = states["se_state0"].as_long()
    u_long_long_64 = (state0 >> 12) | 0x3FF0000000000000
    float_64 = struct.pack("<Q", u_long_long_64)
    next_sequence = struct.unpack("d", float_64)[0]
    next_sequence -= 1

现在就有一个可以破解Math.random函数的脚本了
脚本完全代码:

#!/usr/bin/python3
import z3,struct,sys

sequence = [0.6199046082820001, 0.6623637813965961, 0.7190181683749095, 0.06169296721449724, 0.915799780594273]

sequence = sequence[::-1]
solver = z3.Solver()
se_state0, se_state1 = z3.BitVecs("se_state0 se_state1", 64)

for i in range(len(sequence)):
    se_s1 = se_state0
    se_s0 = se_state1
    se_state0 = se_s0
    se_s1 ^= se_s1 << 23
    se_s1 ^= z3.LShR(se_s1, 17)
    se_s1 ^= se_s0
    se_s1 ^= z3.LShR(se_s0, 26)
    se_state1 = se_s1

    float_64 = struct.pack("d", sequence[i] + 1)
    u_long_long_64 = struct.unpack("<Q", float_64)[0]
    mantissa = u_long_long_64 & ((1 << 52) - 1)
    solver.add(int(mantissa) == z3.LShR(se_state0, 12))

if solver.check() == z3.sat:
    model = solver.model()

    states = {}
    for state in model.decls():
        states[state.__str__()] = model[state]

    state0 = states["se_state0"].as_long()
    u_long_long_64 = (state0 >> 12) | 0x3FF0000000000000
    float_64 = struct.pack("<Q", u_long_long_64)
    next_sequence = struct.unpack("d", float_64)[0]
    next_sequence -= 1

    print(next_sequence)

运行这个脚本，获得下一个随机数

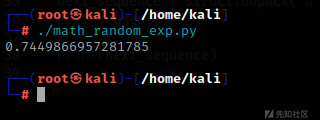
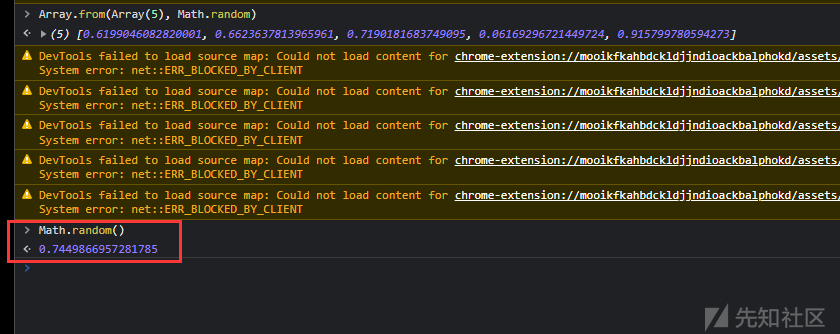
成功正确预测了下一个随机数