文章 - crypto-离散对数BSGS(大步小步算法)

1、离散对数问题

离散对数问题是一个在密码学和数论中非常重要的问题。简单来说，离散对数问题就是在给定的群（比如整数模n的乘法群）中，找到一个数x，使得某个元素g的x次方等于另一个给定的元素h，即求解方程：

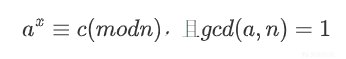
这里的a和c是群中的元素，n是群的阶（对于模n的乘法群，n就是模数），x就是我们要找的离散对数。

为了解决这个问题，我们可以使用不同的算法，但请注意，当n是一个非常大的质数时，这个问题变得非常困难，这也是很多密码系统安全性的基础。

下面是一些解决离散对数问题的方法：

穷举法：

这是最简单直接的方法，就是尝试所有可能的x值，毫无技巧可言，但同时因为费马小定理a^{φ(n)}= 1modn,所以我们其实只要试到φ(n)就好了，如果n为素数，也就只要到n-1就行了。

当然如果当n很大时，这种方法是不切实际的，因为它的时间复杂度是指数级的。
Shanks的小步大步算法（Baby-Step Giant-Step Algorithm）：

这是一种更高效的算法，用于解决离散对数问题。它的基本思想是将可能的x值范围分成“小步”和“大步”，然后通过比较来找到正确的x值。这种方法的时间复杂度比穷举法要好得多。
其他还有Pollard's Rho算法、数域筛法（Number Field Sieve, NFS）、量子算法等算法，今天就不单独讲了。

下面来介绍一下今天的主角：BSGS(大步小步算法)

2、BSGS算法及原理

2-1、将x拆成"大步"和"小步"

BSGS（Baby-Step Giant-Step）算法，正如其名，是通过将未知的离散对数x分解为kp-q的形式用于解决问题，这里的k是一个我们选择的参数，通常取$\sqrt n$，记住以下具体原因后面会讲。

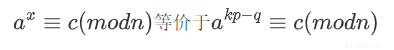
并且满足以下条件：

大步：0<p<[n/k],这里的[n/k]表示向上取n/k，就是3.5取4的意思，所以kp>=n
小步：0<q<k

2-2、等式变换

为了方便解这个方程，我们可以将其改写，先将a拆成两部分

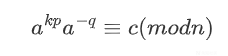
由于我们是在模n的环境下运算，需要可以利用模逆元的概念（如果a和n互质，则a存在模n的乘法逆元）。为了得到一个更易于处理的形式，我们可以两边同时乘以a**q，得到：

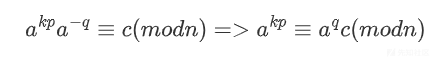
现在方程已经转换为一个更易于处理的形式。

2-3、大步小步求解（算法核心）

根据上面我们已经处理好的式子，我们现在开始算法核心

2-3-1、小步（Baby Steps）

首先，我们执行小步阶段。对于q我们从0到k-1遍历的每一个值计算$a^qcmodn$，并将这些结果存储在一个哈希表（或字典）中，就要求一一对应,其中键是计算的结果，值是对应的q。

2-3-2、大步（Giant Steps）

接下来，我们进入大步阶段。对于p从0到⌈n/k⌉的每一个值（这里⌈n/k⌉表示向上取整），我们计算$a^{kp}modn$。

然后，我们在哈希表（或字典）中查找这个计算结果。如果找到了匹配的值，那么我们就找到了一个解，其中p是当前的大步迭代值，而q是从哈希表中检索到的对应值。

如果没有找到匹配的值，则继续增加p的值并重复此大步过程。

2-3-3、输出结果

如果找到了解，则返回解x=kp-q，需要注意的是，由于我们在模运算中工作，因此如果x是负数，我们需要通过加上n的适当倍数来将其转换为非负数。

如果在遍历了所有可能的p值后仍然没有找到解，则我们可以确定原方程在给定范围内无解。

2-4、关于如何取k

上面我们简要了解了BSGS算法的基本流程和原理，可以看出，关键参数k的取值对算法的性能有着显著影响。为了更深入地探讨这一点，我们可以从算法的时间复杂度出发，来分析k的最佳取值。

在BSGS算法中，时间复杂度主要由两部分构成：小步阶段的计算和大步阶段的查找。小步阶段需要计算并存储(k)个值，时间复杂度为(O(k))；而大步阶段最多需要进行(n/k)次查找，每次查找的时间复杂度可以认为是常数（假设哈希表操作是常数时间的），所以大步阶段的时间复杂度为(O(n/k))。

因此，总的时间复杂度可以表示为：

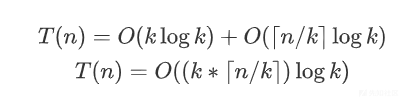
为了最小化这个时间复杂度，我们需要找到一个合适的(k)值。通过高中学习的均值不等式x^2+y^2>=2xy,这时这两个部分的时间复杂度达到平衡，从而使得总的时间复杂度最小：

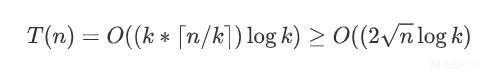
所以，从优化算法性能的角度出发$k=\sqrt n$时才取最小值，也就是时间复杂度最小。

脚本

import math

def bsgs(a, c, n):
    assert math.gcd(a, n) == 1, "a and P must be coprime"

    K = int(math.ceil(math.sqrt(n)))
    right_values = {}
    rv = c % n

    # Precompute right values
    for q in range(1,K):
        rv = (rv * a) % n
        right_values[rv] = q


    ak = pow(a, K, n)

    # Search for solution
    for p in range(1,K):
        left = pow(ak, p, n)
        if left in right_values:
            q = right_values[left]
            X = p * K - q
            return X

    return None

# Example usage:
a = 17
c = 5
n = 23
x = bsgs(a, c, n)
if x is not None:
    print(f"Found x = {x}")
else:
    print("No solution found.")
#Found x = 19

3、EXBSGS(算法拓展)

上面我们基本介绍了一下BSGS算法的基本原理，同时还提到了a与n要互质(否则求不了逆元)才能使用，为了使算法的应用范围更广，我们对原本的算法进行一个拓展用于解决当底数a和模数n不互质时求离散对数的问题。

处理步骤

我们的基本思路是将不互素的a和n处理一下使他们变成能使用bsgs的形式

计算最大公约数：首先，我们先计算出a和n的最大公约数g=gcd（a，n）
检查无解情况：如果c不能被g整除，则方程无解，这里因为a和n有公因数g，所以c一定是有的。
更新变量：如果c能被g整除，就则更新变量，c=c/g,p=p/g

并记录下除g的次数。（这里a不要更新，只要记住次数就行了）

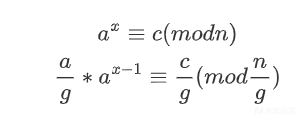
如果此时a和n仍然不互质,继续进行以上操作，直到a和n互质

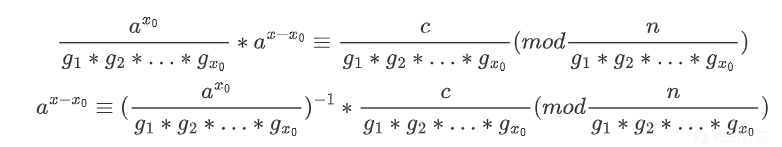
我们现在就将$a^{x-x0}$看作a^x,右侧的式子看作c，来进行BSGS算法，这里得到的x要再加上x0

import math

import gmpy2
from sympy import symbols, Eq, solve

def bsgs(a, c, P):
    assert math.gcd(a, P) == 1, "a and P must be coprime"

    K = int(math.ceil(math.sqrt(P)))
    right_values = {}
    rv = c % P

    # Precompute right values
    for q in range(1,K):
        rv = (rv * a) % P
        right_values[rv] = q


    ak = pow(a, K, P)

    # Search for solution
    for p in range(1,K):
        left = pow(ak, p, P)
        if left in right_values:
            q = right_values[left]
            X = p * K - q
            return X

    return None

def exbsgs(a, c, p):
    a0=a
    c0=c
    p0=p
    # Initialize
    x0 = 0
    d=1
    # Make a and p coprime
    g = math.gcd(a0, p)
    while g != 1:
        if c % g != 0:
            return None  # No solution
        x0 = x0 + 1
        c = c // g
        p = p // g
        a = a // g
        d*=g
        g = math.gcd(a0, p)
    al=a0**x0//d
    a1=gmpy2.invert(al,p)
    c=c*a1%p
    x=bsgs(a0,c,p)+x0
    return x



# Example usage:
a = 6
c =42
p = 58
x = exbsgs(a, c, p)
print(x)
if x is not None:
    print(f"Found x = {x}")
else:
    print("No solution found.")
#34