文章 - CTF_Crypro_PRNG浅析

在ctf中比较常见的流密码题型中lcg,mt19937,lfsr三类伪随机数生成方法是比较常见的,本文对这三类做一个介绍并附上一些简单的例子

lcg

原理

lcg即线性同余生成器，是较为简单的伪随机数生成方法，通常由如下式子生成

作为题目出现时，通常是已知这个式子里的几个量，需要求这个式子里余下的几个未知量

1.求a

a=((Xn+2-Xn+1)(Xn+1-Xn)^(-1))%m

2.求b

b=(Xn+1 - aXn)%m

3.求m

tn=Xn+1-Xn，m=gcd((tn+1tn-1 - tntn) , (tntn-2 - tn-1tn-1))

4.已知Xn+1求Xn

Xn=((Xn+1 - b)a^(-1))%m

例题

LitCTF2023babyLCG

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
bit_len = m.bit_length()
a = getPrime(bit_len)
b = getPrime(bit_len)
p = getPrime(bit_len+1)

seed = m
result = []
for i in range(10):
    seed = (a*seed+b)%p
    result.append(seed)
print(result)

分析

seed=m，所以要求出a,b,p从而求出seed得到flag,就是上面那几个公式的应用

exp

import gmpy2
from Crypto.Util.number import *
result = []
t = []
for i in range(len(result)-1):
    t.append(result[i]-result[i-1])
for i in range(len(result)-3):
    p = gmpy2.gcd((t[i + 1] * t[i - 1] - t[i] * t[i]), (t[i + 2] * t[i] - t[i + 1] * t[i + 1]))
    try:
        a = (gmpy2.invert(result[8] - result[7], p) * (result[9] - result[8])) % p
        b = (result[9] - a * result[8]) % p
        seed = (result[0] - b) * gmpy2.invert(a, p) % p
        print(long_to_bytes(seed))
    except:
        continue

mt19937

原理

mt19937即是梅森旋转方法，简称mt，可以产生32位整数序列。具有以下的优点

代码实现(32位)：

def _int32(x):
    return int(0xFFFFFFFF & x)

class MT19937:
    # 根据seed初始化624的state
    def __init__(self, seed):
        self.mt = [0] * 624
        self.mt[0] = seed
        self.mti = 0
        for i in range(1, 624):
            self.mt[i] = _int32(1812433253 * (self.mt[i - 1] ^ self.mt[i - 1] >> 30) + i)

    # 提取伪随机数
    def extract_number(self):
        if self.mti == 0:
            self.twist()
        y = self.mt[self.mti]
        y = y ^ y >> 11
        y = y ^ y << 7 & 2636928640
        y = y ^ y << 15 & 4022730752
        y = y ^ y >> 18
        self.mti = (self.mti + 1) % 624
        return _int32(y)

    # 对状态进行旋转
    def twist(self):
        for i in range(0, 624):
            y = _int32((self.mt[i] & 0x80000000) + (self.mt[(i + 1) % 624] & 0x7fffffff))
            self.mt[i] = (y >> 1) ^ self.mt[(i + 397) % 624]

            if y % 2 != 0:
                self.mt[i] = self.mt[i] ^ 0x9908b0df

例题

题目

伪随机数预测

import random
from Crypto.Cipher import AES
def padding(str):
    while len(str) < 16:
        str += b'\x00'
    return str
flag = b'flag{xxxxx}' #you need to solve this.
f = open("output.txt",'w')
for i in range(624):
    f.write(str(random.getrandbits(32)))
    f.write('\n')
key = padding(str(random.getrandbits(32)).encode())
aes = AES.new(key,AES.MODE_ECB)
cip = aes.encrypt(flag)
print(cip)

分析

如题第625个伪随机数是aes的key，需要预测下一个伪随机数，使用RandCrack

exp

from randcrack import RandCrack
from Crypto.Cipher import AES

cip = b''
def padding(str):
    while len(str) < 16:
        str += b'\x00'
    return str

with open(r"output.txt", 'r') as f:
    random_numbers = [int(line.strip()) for line in f]

rc = RandCrack()
for num in random_numbers:
    rc.submit(num)

next_random_number = rc.predict_getrandbits(32)
print("Predicted next random number:", next_random_number)

key = padding(str(next_random_number).encode())
aes = AES.new(key,AES.MODE_ECB)
flag = aes.decrypt(cip)
print(flag)

[SUCTF2019]MT

考点：逆向 extract_number函数

from Crypto.Random import random
from Crypto.Util import number
from flag import flag

def convert(m):
    m = m ^ m >> 13
    m = m ^ m << 9 & 2029229568
    m = m ^ m << 17 & 2245263360
    m = m ^ m >> 19
    return m

def transform(message):
    assert len(message) % 4 == 0
    new_message = ''
    for i in range(len(message) / 4):
        block = message[i * 4 : i * 4 +4]
        block = number.bytes_to_long(block)
        block = convert(block)
        block = number.long_to_bytes(block, 4)
        new_message += block
    return new_message

transformed_flag = transform(flag[5:-1].decode('hex')).encode('hex')
print 'transformed_flag:', transformed_flag
# transformed_flag: 641460a9e3953b1aaa21f3a2

分析

def convert(m):
    m = m ^ m >> 13
    m = m ^ m << 9 & 2029229568
    m = m ^ m << 17 & 2245263360
    m = m ^ m >> 19
    return m

看一下这里的convert函数可以发现就是原本实现中的extract_number函数的一部分，且transform函数的加密过程也以convert为核心(几乎就只是调用了一下convert)，那么只要将这个函数逆向一下就可以得到flag了

exp

#python2
from Crypto.Util import number

# right shift inverse
def inverse_right(res, shift, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp >> shift
    return tmp


# right shift with mask inverse
def inverse_right_mask(res, shift, mask, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp >> shift & mask
    return tmp

# left shift inverse
def inverse_left(res, shift, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp << shift
    return tmp


# left shift with mask inverse
def inverse_left_mask(res, shift, mask, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp << shift & mask
    return tmp


def extract_number(y):
    y = y ^ y >> 11
    y = y ^ y << 7 & 2636928640
    y = y ^ y << 15 & 4022730752
    y = y ^ y >> 18
    return y&0xffffffff

def convert(y):
    y = inverse_right(y,19)
    y = inverse_left_mask(y,17,2245263360)
    y = inverse_left_mask(y,9,2029229568)
    y = inverse_right(y,13)
    return y&0xffffffff

def transform(message):
    assert len(message) % 4 == 0
    new_message = ''
    for i in range(len(message) / 4):
        block = message[i * 4 : i * 4 +4]
        block = number.bytes_to_long(block)
        block = convert(block)
        block = number.long_to_bytes(block, 4)
        new_message += block
    return new_message

transformed_flag = '641460a9e3953b1aaa21f3a2'
c = transformed_flag.decode('hex')
flag = transform(c)
print flag.encode('hex')

lfsr

原理

移位寄存器(ShiftRegister，SR)

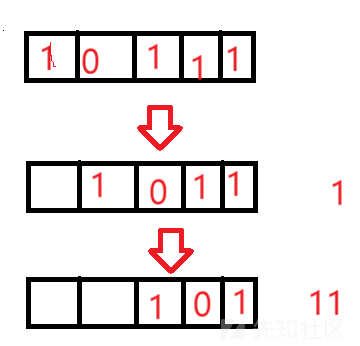
如图所示，移位寄存器指把x个寄存器排列为一行(就是数据结构里的顺序队列)，然后把队首的寄存器的数值传递出去，其余每一个数值前进一位

反馈移位寄存器(Feedback Shift Register，FSR)

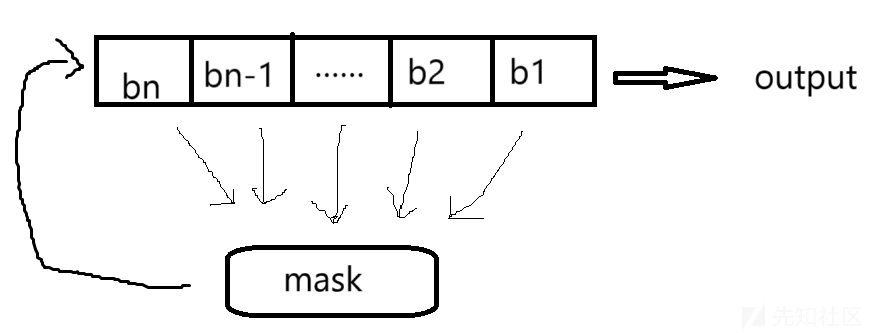
如图，每次把最后一位移位出去之后就必然会导致缺少队列里面减少一位，反馈移位寄存器就解决了这个问题，解决这个问题的方式是使用寄存器里面的所有的n个数值来获取一个新的值并填充在队列的队尾(划重点)

线性反馈移位寄存器(Linear Feedback Shift Register，LFSR)

lfsr就是在fsr的基础上确保了用来生成新的数值的反馈函数是一个与b1,b2,……,bn-1,bn,这n个数值都相关的线性函数(也就是n元一次方程这样子)
图可以看下下面那道B-M题的分析部分的那幅图
除此之外还有nfsr(也就是非线性的，不过还没遇到相关的题目)
注：lfsr通常是在GF(2)上的,也就是数值只能是0or1
通常题型是已知反馈函数(mask)、初始状态和输出序列这三者中的一部分，然后求出藏在其他部分的flag

B-M算法

如果我们知道了长度为 2n 的连续的输出序列(n位初始状态+n位输出序列也行，只要是连续的2n位就行)，那么就可以通过构造矩阵来求出 mask,时间复杂度：$O(n^2)$ 次比特操作,空间复杂度：$O(n)$ 比特

例题

题目

B-M算法

import hashlib
from secret import KEY,FLAG,MASK
assert(FLAG=="de1ctf{"+hashlib.sha256(hex(KEY)[2:].rstrip('L')).hexdigest()+"}")
assert(FLAG[7:11]=='1224')
LENGTH = 256
assert(KEY.bit_length()==LENGTH)
assert(MASK.bit_length()==LENGTH)
def pad(m):
    pad_length = 8 - len(m)
    return pad_length*'0'+m
class lfsr():
    def __init__(self, init, mask, length):
        self.init = init
        self.mask = mask
        self.lengthmask = 2**(length+1)-1

    def next(self):
        nextdata = (self.init << 1) & self.lengthmask 
        i = self.init & self.mask & self.lengthmask 
        output = 0
        while i != 0:
            output ^= (i & 1)
            i = i >> 1
        nextdata ^= output
        self.init = nextdata
        return output
if __name__=="__main__":
    l = lfsr(KEY,MASK,LENGTH)
    r = ''
    for i in range(63):
        b = 0
        for j in range(8):
            b = (b<<1)+l.next()
        r += pad(bin(b)[2:])
    with open('output','w') as f:
        f.write(r)

分析

这题中输出序列只给出了504个值，根据 B-M 算法，我们需要确定512个值（因为这里lfsr的度n为256，所以需要512位）来求出mask，这里可以使用爆破最后8位的方法，再用爆破出来的这些输出序列恢复出mask的值，然后筛选得到mask
恢复mask：
已知512位连续的序列，mask为256位的序列，可以直接构建出一个256元一次方程组来求解mask，这个方程组也可以直接看作是一个矩阵
具体方程组参照下图

注：这里的*是模2乘的意思，也简单的看作直接异或
~~(检查的时候突然发现图里这个*不是很贴切)~~

exp

#sage
import hashlib

key = ''

#将二进制数据填充为8位
def pad(x):
    pad_length = 8 - len(x)
    return '0'*pad_length+x  

# 获取 256个 key 可能值
def get_key(mask,key):
    R = ""
    index = 0
    key = key[255] + key[:256]
    while index < 256:
        tmp = 0
        for i in range(256):
            if mask >> i & 1:
                # tmp ^= int(key[255 - i])
                tmp = (tmp+int(key[255-i]))%2
        R = str(tmp) + R
        index += 1
        key = key[255] + str(tmp) + key[1:255]
    return int(R,2)

# 将二进制流转化为十进制
def get_int(x):
    m=''
    for i in range(256):
        m += str(x[i])
    return (int(m,2))

# 获取到256个 mask 可能值，再调用 get_key()函数，获取到key值，将结果导入到 sm 中
sm = []
for pad_bit in range(2**8):   #爆破rr中缺失的8位
    r = key+pad(bin(pad_bit)[2:])
    index = 0
    a = []
    for i in range(len(r)):
        a.append(int(r[i]))       #将 r 转换成列表a = [0,0,1,...,]格式    
    res = []
    for i in range(256):
        for j in range(256):
            if a[i+j]==1:
                res.append(1)
            else:
                res.append(0)
    sn = []
    for i in range(256):
        if a[256+i]==1:
            sn.append(1)
        else:
            sn.append(0)
    MS = MatrixSpace(GF(2),256,256)        #构造 256 * 256 的矩阵空间
    MSS = MatrixSpace(GF(2),1,256)         #构造 1 * 256 的矩阵空间
    A = MS(res)
    s = MSS(sn)                       #将 res 和 sn 的值导入矩阵空间中
    try:
        inv = A.inverse()            # 求A 的逆矩阵
    except ZeroDivisionError as e:
        continue
    mask = s*inv                     #构造矩阵求mask，B-M 算法
#     print(mask[0])                  #得到 256 个 mask 值()，type元组
#     print(get_int(mask[0]))
#     print(key_list)
#     print(key[:256])
#     print(hex(solve(get_int(mask[0]),key[:256])))
#     break   
    sm.append(hex(get_key(get_int(mask[0]),key[:256]))) 

# 通过限制条件确定 最终 的flag值
for i in range(len(sm)):
    FLAG = hashlib.sha256(sm[i][2:].encode()).hexdigest()
    if FLAG[:4]=='1224':
        print('flag{'+FLAG+'}')