文章 - 2024 0xGame Week1 密码 wp

[Week 1] Caesar Cipher

密文：0yHbnf{Uif_Cfhjoojoh_Pg_Dszqup}
提示：凯撒加密。

正常我们都会想flag的形式应该是0xCTF之类的，看密文可以知道应该是前移1位，于是我们用工具跑一下就能得到：

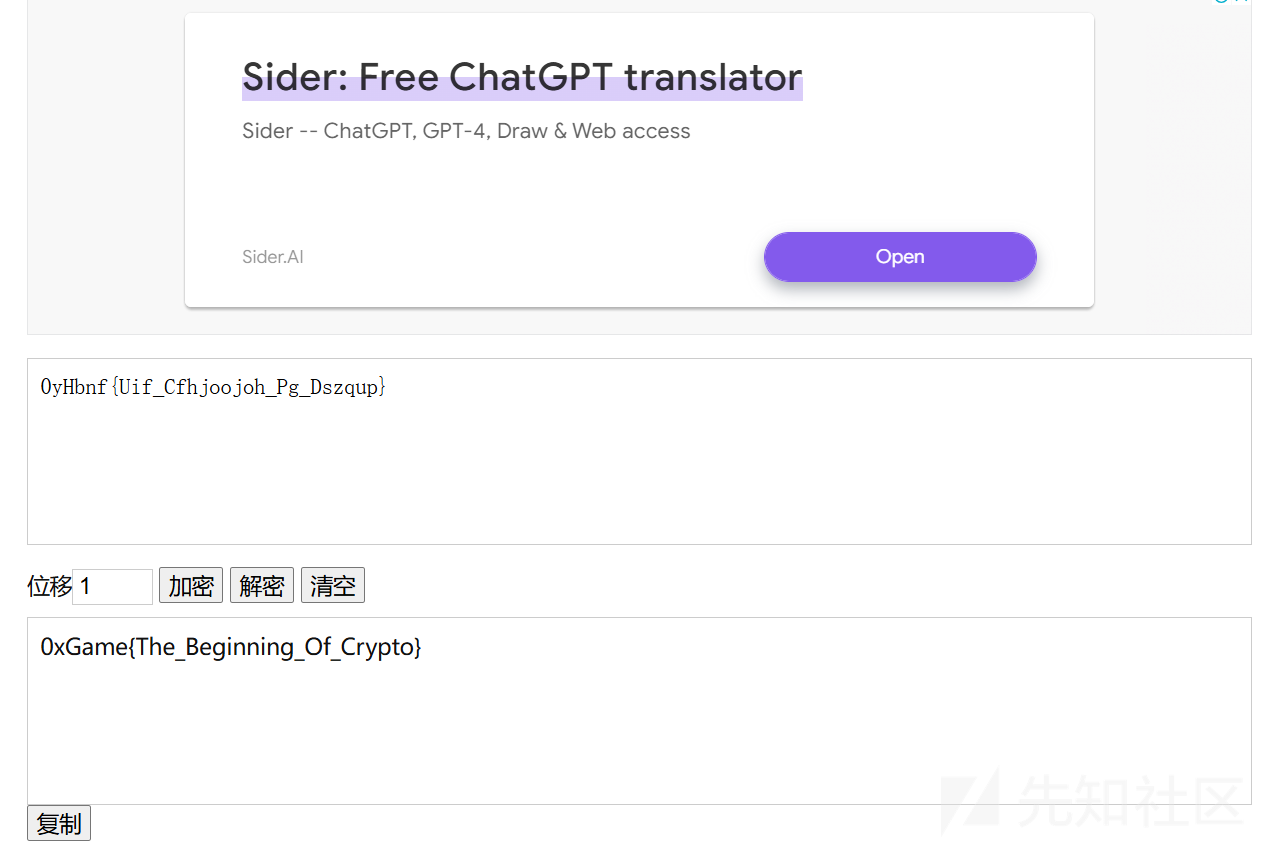
0xGame{The_Beginning_Of_Crypto}

工具网址：凯撒密码在线加密解密 - 千千秀字 (qqxiuzi.cn)

[Week 1] Code

#How to use mathematics to represent information?
from Crypto.Util.number import bytes_to_long
from base64 import b64encode
from secret import flag

msg = flag.encode()
length = len(msg)

assert length%4 == 0
block = length//4
m = [ msg[ block*(i) : block*(i+1) ] for i in range(4) ]

m0 = m[0]
m1 = bytes_to_long(m[1])
m2 = m[2].hex()
m3 = b64encode(m[3])

print(f'm0 = {m0}\nm1 = {m1}\nm2 = {m2}\nm3 = {m3}')
'''
m0 = b'0xGame{73d7'
m1 = 60928972245886112747629873
m2 = 3165662d393339332d3034
m3 = b'N2YwZTdjNGRlMX0='
'''

这道题目非常巧妙地通过一个简单的 flag 处理过程，展示了 CTF 中常见的几种编码和转换操作。通过此题，选手不仅可以理解如何将不同的数据格式相互转换，还能加深对基础密码学的一些函数认识。我也借此给大家介绍一下：

bytes_to_long 函数：

这个函数来自 Crypto.Util.number模块，通常用于将字节串转换为长整数。它在 CTF 题目中非常常见，尤其是在 RSA 等需要将字符串消息转换成整数来进行加密或解密的场景下。
在代码中，m1 通过 bytes_to_long将第二块数据转换为长整数。
bytes_to_long为上一个函数的逆操作。

base64 编码：

b64encode是 Base64 编码的标准库函数，Base64 在传输二进制数据时非常常见，因为它将数据编码为 ASCII 字符串，易于传输。
这里的 m3使用了 b64encode来对第四块数据进行 Base64 编码，输出结果就是一串 Base64 编码后的字符串。
同样b64decode就是解密函数。

hex 编码：

m2 的处理则是直接使用 .hex()方法，将bytes字节数据转换为其对应的十六进制字符串。这种转换在许多加密题目中都很常见，用来将原始数据表示为可读的形式。
这种十六进制编码方式经常用于显示或储存原始字节数据，如在哈希算法或密钥处理场景中。exp:

from Crypto.Util.number import *
from base64 import b64decode
m0 = b'0xGame{73d7'
m1 = 60928972245886112747629873
m2 = 0x3165662d393339332d3034
m3 = b'N2YwZTdjNGRlMX0='

M0=m0
M1=long_to_bytes(60928972245886112747629873)
M2=long_to_bytes(m2)#因为十六进制还是数字，可以直接转bytes
M3=b64decode(m3)

print(M0+M1+M2+M3)
#b'0xGame{73d72f64-7656-11ef-9393-047f0e7c4de1}'

[Week 1] Code-Vigenere

from secret import flag
from os import urandom
from base64 import b64encode

def Encrypt(msg, key):
    Lenth = len(key)
    result = ''

    upper_base = ord('A')
    lower_base = ord('a')
    KEY = [ord(key.upper()[_]) - upper_base for _ in range(Lenth)]

    index = 0
    for m in msg:
        tmp_key = KEY[index%Lenth] 
        if not m.isalpha():
            result += m
            continue

        if m.isupper(): 
            result += chr(upper_base + (ord(m) - upper_base + tmp_key) % 26)
        else: 
            result += chr(lower_base + (ord(m) - lower_base + tmp_key) % 26)
        index += 1
    return result

key = b64encode(urandom(6))[:5].decode()
print(Encrypt(flag,key))

#0lCcop{oyd94092-g8mq-4963-88b6-4helrxdhm6q7}

我们知道维吉尼亚密码通过将明文的每个字母与一个重复的密钥字母表对应，进行字母表上的循环位移加密。其核心是按字母位置的偏移，使得密钥字母对应的位移量作用于明文字母，产生密文。就像C+V=X，就是按照下表来加密。

于是我们就能通过密文和flag头0xGame来推测密钥得到，密钥为owccl，再用解密网站解密解密得到：

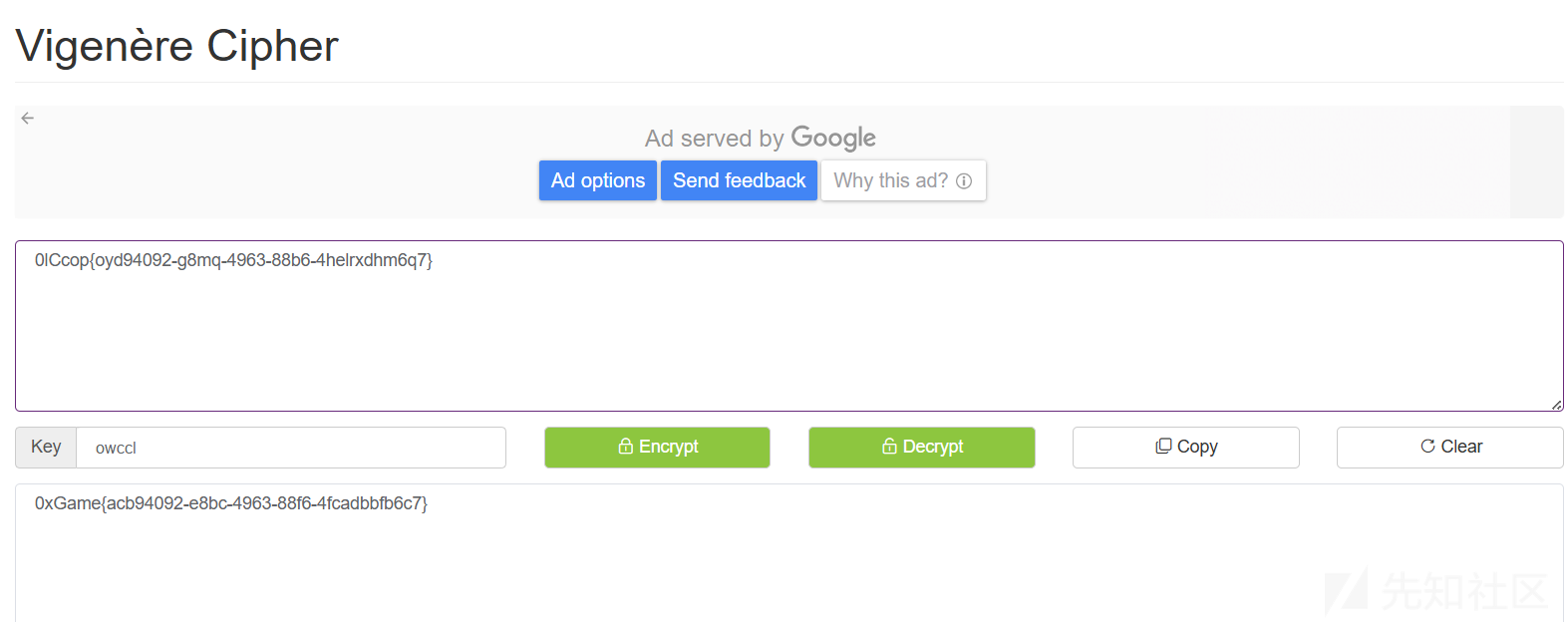
0xGame{acb94092-e8bc-4963-88f6-4fcadbbfb6c7}

解密网站：Vigenère Cipher - A.Tools

[Week 1] RSA-Baby

from Crypto.Util.number import bytes_to_long, getPrime
from hashlib import md5
from random import randint
from gmpy2 import invert,gcd

#Hash Function:
def MD5(m):return md5(str(m).encode()).hexdigest()

#RSA AlgorithmParameter Generation Function:
def KeyGen():
    Factor_BitLength = 30
    q = getPrime(Factor_BitLength)
    p = getPrime(Factor_BitLength)
    N = p * q
    #Euler's totient function:
    phi = (p-1) * (q-1)

    #Generate Keys:
    while True:
        e = randint(1,phi)
        if gcd(e,phi) == 1:
            d = int(invert(e,phi))
            break

    #Generate Result:
    Pub_Key = (N,e)
    Prv_Key = (N,d)
    return Pub_Key,Prv_Key

Pub,Prv = KeyGen()

N = Pub[0]
e = Pub[1]
d = Prv[1]

#RSA Encrypt:
m = randint(1,N)
c = pow(m,e,N)

print(f'Pub_Key = {Pub}')
print(f'Prv_Key = {Prv}')
print(f'Encrypt_msg = {c}')

'''
Pub_Key = (547938466798424179, 80644065229241095)
Prv_Key = (547938466798424179, 488474228706714247)
Encrypt_msg = 344136655393256706
'''

flag = '0xGame{'+ MD5(m) +'}'

这道题与其说是让我们解密，不认识是在教我们学习逆元是什么。

在我们平时应用的运算规律也就是普通的乘法中，两个数相乘等于1时，我们说其中一个数是另一个数的倒数(也可以说是乘法逆元)。比如， 5×1/5 = 1/5×5/1=1，那么 1/5就是5的倒数(也可以说是乘法逆元)。

然而在模运算下的逆元下。对于一个整数a和一个模数 n，如果存在一个数b，使得 a×bmod n=1,a*b mod n= 1，那么 b 就是 a 在模 n 下的乘法逆元。找到这个 b就叫求逆元。

简单来说，逆元就是那个在某种运算（比如模运算）下能让结果“变成1”的数。当然这个说的比较局限，但在我们密码学里的模运算下可以怎么理解。

回到这道题，我们可以看出e和d在phi_n下互为逆元，于是可以根据RSA的原理得到m

exp：

from hashlib import md5

def MD5(m):return md5(str(m).encode()).hexdigest()

Prv_Key = (547938466798424179, 488474228706714247)
Encrypt_msg = 344136655393256706

N = Prv_Key[0]
d = Prv_Key[1]

c = Encrypt_msg
m = pow(c, d, N)
flag = '0xGame{'+ MD5(m) +'}'

print(flag)
#0xGame{6e5719c54cdde25ce7124e280803f938}

[Week 1] RSA-Easy

from Crypto.Util.number import bytes_to_long, getPrime
from hashlib import md5
from random import randint
from gmpy2 import invert,gcd

#Hash Function:
def MD5(m):return md5(str(m).encode()).hexdigest()

#RSA AlgorithmParameter Generation Function:
def KeyGen():
    Factor_BitLength = 30
    q = getPrime(Factor_BitLength)
    p = getPrime(Factor_BitLength)
    N = p * q
    #Euler's totient function:
    phi = (p-1) * (q-1)

    #Generate Keys:
    while True:
        e = randint(1,phi)
        if gcd(e,phi) == 1:
            break

    #Generate Result:
    Pub_Key = (N,e)
    return Pub_Key

Pub = KeyGen()

N = Pub[0]
e = Pub[1]

#RSA Encrypt:
m = randint(1,N)
c = pow(m,e,N)

print(f'Pub_Key = {Pub}')
print(f'Encrypt_msg = {c}')

'''
Pub_Key = (689802261604270193, 620245111658678815)
Encrypt_msg = 289281498571087475
'''

flag = '0xGame{'+ MD5(m) +'}'

每次我们说到密码原理都会说到，加密算法之所以能够有效地保护数据的安全，其核心在于一个难以解决的数学问题。这个数学问题的难易程度直接决定了加密算法的加密强度。而就如这道题目说的就如题目提示说：RSA为什么安全？RSA的加密强度是基于大素数分解的，如果我们能够分解出n，就能得到n对应的欧拉函数phi_n，进而得到d，解出RSA就不是问题了。所以我们需要做的就是分解n。主要的方法就是用网站以及yafu

网站http://factordb.com/
yafu可以把整数因数分解，在RSA中，当p、q的取值差异过大或过于相近的时候，使用yafu可以快速的把n值分解出p、q值，相当于一个线下的程序，适合在没网的场合使用。

结果为：

689802261604270193=823642439*837502087

分解出了n就很简单了

import gmpy2
from hashlib import md5

def MD5(m):return md5(str(m).encode()).hexdigest()

p=823642439
q=837502087
e=620245111658678815
c=289281498571087475

n=p*q
phi_n =(p-1)*(q-1)
d = gmpy2.invert(e, phi_n)
m = gmpy2.powmod(c, d, n)

flag = '0xGame{'+ MD5(m) +'}'
print(flag)
#0xGame{5aa4603855d01ffdc5dcf92e0e604f31}

[Week 1] Number-Theory-CRT

from Crypto.Util.number import bytes_to_long, getPrime
from hashlib import md5
from random import randint
from gmpy2 import invert,gcd

#Hash Function:
def MD5(m):return md5(str(m).encode()).hexdigest()

#RSA AlgorithmParameter Generation Function:
def KeyGen():
    Factor_BitLength = 30
    q = getPrime(Factor_BitLength)
    p = getPrime(Factor_BitLength)
    N = p * q
    #Euler's totient function:
    phi = (p-1) * (q-1)

    #Generate Keys:
    e = randint(1,phi)

    #Generate Result:
    Pub_Key = (N,e)
    return Pub_Key

Pub = KeyGen()

N = Pub[0]
e = Pub[1]

#RSA Encrypt:
m = randint(1,N)
c = pow(m,e,N)

print(f'Pub_Key = {Pub}')
print(f'Encrypt_msg = {c}')

'''
Pub_Key = (1022053332886345327, 294200073186305890)
Encrypt_msg = 107033510346108389
'''

flag = '0xGame{'+ MD5(m) +'}'

看起来是一道简单的RSA题目，我们先分解n看看：

1022053332886345327=970868179 · 1052721013

网站：factordb.com

然后用普通的RSA解密却发现解不了，发现e和phi互素，于是就想到了我之前写过的AMM算法。另外说一下，这道题目的数据有点特殊，所以常规开e与phi公因数方的方法用不了，所以还是用AMM方便一点。

exp:

import random
import time
from tqdm import tqdm
from Crypto.Util.number import *
import gmpy2
from hashlib import md5

#Hash Function:
def MD5(m):return md5(str(m).encode()).hexdigest()
def AMM(o, r, q):
    start = time.time()
    print('\n----------------------------------------------------------------------------------')
    print('Start to run Adleman-Manders-Miller Root Extraction Method')
    print('Try to find one {:#x}th root of {} modulo {}'.format(r, o, q))
    g = GF(q)
    o = g(o)
    p = g(random.randint(1, q))
    while p ^ ((q-1) // r) == 1:
        p = g(random.randint(1, q))
    print('[+] Find p:{}'.format(p))
    t = 0
    s = q - 1
    while s % r == 0:
        t += 1
        s = s // r
    print('[+] Find s:{}, t:{}'.format(s, t))
    k = 1
    while (k * s + 1) % r != 0:
        k += 1
    alp = (k * s + 1) // r
    print('[+] Find alp:{}'.format(alp))
    a = p ^ (r**(t-1) * s)
    b = o ^ (r*alp - 1)
    c = p ^ s
    h = 1
    for i in range(1, t):
        d = b ^ (r^(t-1-i))
        if d == 1:
            j = 0
        else:
            print('[+] Calculating DLP...')
            j = - discrete_log(d, a)
            print('[+] Finish DLP...')
        b = b * (c^r)^j
        h = h * c^j
        c = c^r
    result = o^alp * h
    end = time.time()
    print("Finished in {} seconds.".format(end - start))
    print('Find one solution: {}'.format(result))
    return result

def onemod(p,r):
    t=random.randint(2,p)
    while pow(t,(p-1)//r,p)==1:
         t=random.randint(2,p)
    return pow(t,(p-1)//r,p)

def solution(p,root,e):
    while True:
        g=onemod(p,e)
        may=[]
        for i in tqdm(range(e)):
            may.append(root*pow(g,i,p)%p)
        if len(may) == len(set(may)):
            return may


def solve_in_subset(ep,p):
    cp = int(pow(c,inverse(int(e//ep),p-1),p))
    com_factors = []
    while GCD(ep,p-1) !=1:
        com_factors.append(GCD(ep,p-1))
        ep //= GCD(ep,p-1)
    com_factors.sort()

    cps = [cp]
    for factor in com_factors:
        mps = []
        for cp in cps:
            mp = AMM(cp, factor, p)
            mps += solution(p,mp,factor)
        cps = mps
    for each in cps:
        assert pow(each,e,p)==c%p
    return cps

p=970868179
q=1052721013
c =  107033510346108389
e=294200073186305890
n = p*q

gcd1=gmpy2.gcd(e,p-1)
gcd2=gmpy2.gcd(e,q-1)


m_p = solve_in_subset(gcd1,p)
m_q = solve_in_subset(gcd2,q)

for mpp in m_p:
    for mqq in m_q:
        m = crt([int(mpp),int(mqq)],[p,q])
        if m<n:
            flag = '0xGame{'+ MD5(m) +'}'
            print(flag)



'''
0xGame{15820afdb9a129e89e40e57f40ff8de9}
0xGame{3932f6728585abbf751a212f69276d3e}
0xGame{f4107420d94cc7037114376d8566d4ef}
0xGame{127016d0be858ef48a99723710ad4d49}
'''