YLCTF2024 ROUND3 crypto 全

QWQ

题目

分析

aaEncode编码，将文本转成了颜文字，使用在线网站解密即可，得到字符LFGEGVCGPNUEA5RTL5DHK3S7O4YXI2C7ORUGSNK7M5QW2M27KFLVC7I=

base32解码得到FALG

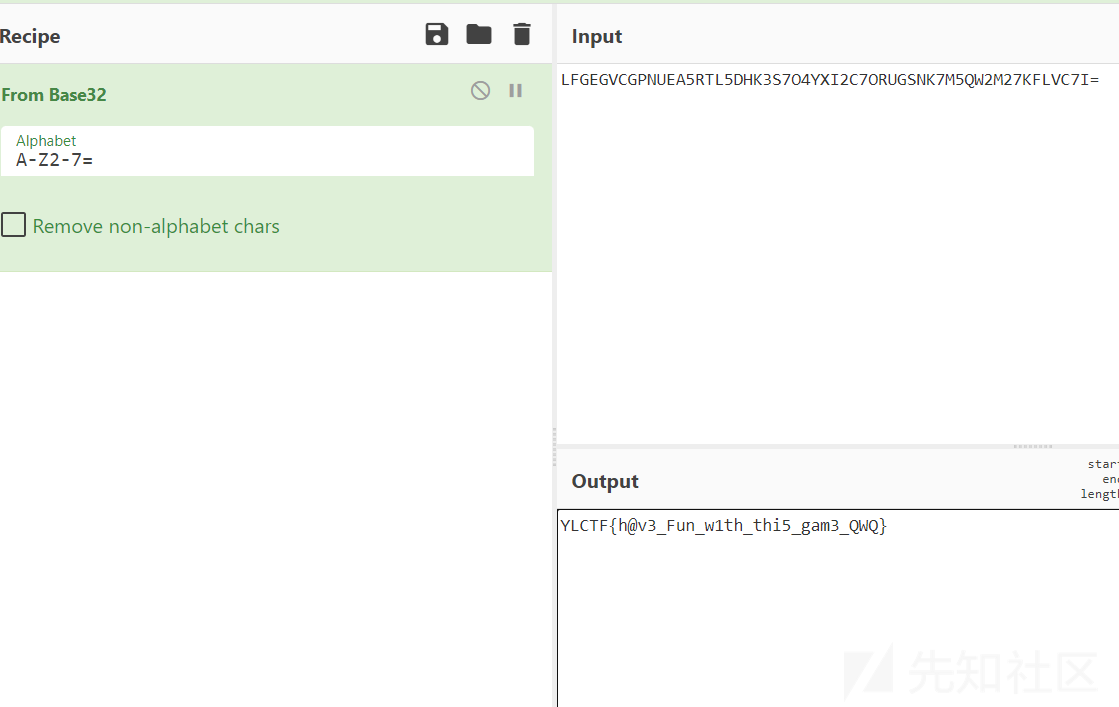
ezlcg

题目

class LCG(object):
    def __init__(self, seed):
        self.N = getPrime(256)
        self.a = randrange(self.N)
        self.b = randrange(self.N)
        self.seed = seed % self.N
        self.state = self.seed

    def next(self):
        self.state = (self.a * self.state + self.b) % self.N
        return self.state

class LCGBoss():

       def __init__(self) -> None:
       key = b""#需要求key
           self.N = getPrime(2048)
           self.a = bytes_to_long(key)
           self.seed = randint(1, self.N-1)

       def next(self):
           self.seed = (self.seed * self.a + randint(-2**114, 2**114)) % self.N
           return self.seed

分析

from pwn import *
from Crypto.Util.number import *
from tqdm import trange
re = remote("challenge.yuanloo.com", 36905)
for i in trange(50):
    re.recvuntil(b"Challenge one,50 Round\n")
    re.recvuntil(b"a=")
    a = int(re.recvuntil(b"\n").decode())
    re.recvuntil(b"b=")
    b = int(re.recvuntil(b"\n").decode())
    re.recvuntil(b"N=")
    N = int(re.recvuntil(b"\n").decode())
    re.recvuntil(b"num1=")
    num1 = int(re.recvuntil(b"\n").decode())
    seed = (num1 - b) * inverse(a, N) % N
    re.sendlineafter(b"seed = ", str(seed).encode())

for i in trange(30):
    re.recvuntil(b"Challenge two,30 Round\n")
    re.recvuntil(b"a=")
    a = int(re.recvuntil(b"\n").decode())
    re.recvuntil(b"N=")
    N = int(re.recvuntil(b"\n").decode())
    re.recvuntil(b"num1=")
    num1 = int(re.recvuntil(b"\n").decode())
    re.recvuntil(b"num2=")
    num2 = int(re.recvuntil(b"\n").decode())
    seed = ((num1 - num2) * inverse(a, N) + num1) % N
    re.sendlineafter(b"seed = ", str(seed).encode())

for i in trange(10):
    re.recvuntil(b"Challenge three,10 Round\n")
    re.recvuntil(b"N=")
    N = int(re.recvuntil(b"\n").decode())
    re.recvuntil(b"num1=")
    num1 = int(re.recvuntil(b"\n").decode())
    re.recvuntil(b"num2=")
    num2 = int(re.recvuntil(b"\n").decode())
    re.recvuntil(b"num3=")
    num3 = int(re.recvuntil(b"\n").decode())
    a = (num2 - num3) * inverse(num1 - num2, N) % N
    seed = ((num1 - num2) * inverse(a, N) + num1) % N
    re.sendlineafter(b"seed = ", str(seed).encode())

re.interactive()

# 100%|██████████| 50/50 [00:12<00:00,  4.09it/s]
# 100%|██████████| 30/30 [00:05<00:00,  5.04it/s]
# 100%|██████████| 10/10 [00:01<00:00,  5.96it/s]
# [*] Switching to interactive mode
# success!
# YLCTF{1a48ac5f-b5e1-4147-b401-c90214a8974c}

repeat

题目

import gmpy2
import libnum

from KEY impory key
n=0xba94dc08d76e6f761431a7d34997a6dec45409b61ed1faea119f1121642a62df
magic_message =  "welcometoYLCTF"

def encode(message,key):
    new_message = magic_message+message  # 拼接flag
    message = new_message.encode("utf-8") # 将字符串转为字节
    length = len(message) # 计算长度
    blocks = [message[i * 16:(i + 1) * 16] for i in range((length + 15) // 16)] # 将密文分组，16个字节一组
    blocks[-1] = blocks[-1].ljust(16, b'\x00') # 将最后一组补齐到16个字节
    c= []
    for i in blocks:
        num = int.from_bytes(i, byteorder='big') # 将字节转为整数
        c_blocak = (num*key*2024)%n # 计算密文
        c.append(c_blocak)
        key -= 0x114514
    encode = b''.join(
        int(c_blocak).to_bytes(32, byteorder='big') for c_blocak in c
    )
    return encode

fp = open("/flag","r")
flag = fp.read()
fp.close()
c = encode(flag,key)
print(c.hex())

分析

import itertools
import string
from sympy.ntheory.modular import crt
from Crypto.Util.number import *
from pwn import *

n = 0xba94dc08d76e6f761431a7d34997a6dec45409b61ed1faea119f1121642a62df
magic_message = "welcometoYLCTF"
# re = remote("challenge.yuanloo.com", 49673)
# c = re.recvline().strip().decode()
# re.close()
c = "28e2f5f44c8e22f6026aaac8425d5bf2b1a225987772212bb45eadd0612ca1ef67dc943928bb4d307eb35dacaec4375427cedba9d3871bb38bbb73bff14b6b1e8bf2bd94b3916697158d64ec8ed021b7b0482b9d5b981140176a1965021d6b164b4a45d63a5809eaad532334a1388f40a9d9959493e3018227afae41873eeb29"
c = bytes.fromhex(c)
print(len(c))
length = len(c)
blocks_c = [c[i * 32:(i + 1) * 32] for i in range((length + 31) // 31)]
for _ in itertools.product(string.printable, repeat=2):
    block0 = magic_message + "".join(_)
    a = bytes_to_long(block0.encode())
    b = bytes_to_long(blocks_c[0])
    key = b * inverse(2024 * a, n) % n
    key -= 0x114514
    for block in blocks_c[1:]:
        c0 = bytes_to_long(block)
        m_block = c0 * inverse(2024 * key, n) % n
        key -= 0x114514
        m = long_to_bytes(m_block).replace(b"\x00", b"").strip()
        try:
            if m.decode().isprintable():

                print(block0, m.decode())
            else:
                break
        except:
            break
# welcometoYLCTFYL CTF{44782ee3-e4d
# welcometoYLCTFYL e-4af0-ae8c-fe82
# welcometoYLCTFYL 64d61ec3}
# welcometoYLCTFYL
# YLCTF{44782ee3-e4de-4af0-ae8c-fe8264d61ec3}

0

题目

from sage.all import ZZ, randint
from Crypto.Util.number import *
p = None

def generate_distortion_map(E):
    if E.a_invariants() != (0,6,0,1,0):
        raise NotImplementedError
    return E.isogeny(E.lift_x(ZZ(1)), codomain=E)

def generate_torsion_points(E, a, b):
    def get_l_torsion_basis(E, l):
        n = (p+1) // l
        return (n*G for G in E.gens())

    P2, Q2 = get_l_torsion_basis(E, 2**a)
    P3, Q3 = get_l_torsion_basis(E, 3**b)

    return P2, Q2, P3, Q3

from flag import flag
flag = bytes_to_long(flag)
def generate_key(E_start, b, P2, Q2, P3, Q3):
    bobs_key = flag
    K = P3 + bobs_key*Q3
    phi = E_start.isogeny(K, algorithm="factored")
    EB = phi.codomain()
    EB.set_order((p+1)**2, num_checks=0)
    PB, QB = phi(P2), phi(Q2)
    return bobs_key, EB, PB, QB


a = 305
b = 192
p = 2^a*3^b - 1
Fp2.<i> = GF(p^2, modulus=x^2+1)
R.<x> = PolynomialRing(Fp2)

E_start = EllipticCurve(Fp2, [0,6,0,1,0])
E_start.set_order((p+1)^2)

two_i = generate_distortion_map(E_start)

P2, Q2, P3, Q3 = generate_torsion_points(E_start, a, b)

flag_key, EB, PB, QB = generate_key(E_start, b, P2, Q2, P3, Q3)

print(EB)
print(PB)
print(QB)

"""
Elliptic Curve defined by y^2 = x^3 + 6*x^2 + (1109655386602666580941477264844188509870568726343453010771770543665511250648180561681677488303290640863245633469198578301207900328491716466654470349910400724631139969542193124833051079*i+2116239248619087101677214169270633679594454755906693836568034229947351325062332338053907457802709748610111020509037164276717020111001082512633925347579357851693517057782645336434230575)*x + (783233241190388171387544682511032475647421068250023300290363249038620119995420899574317207343308349718411589404085433006020673690798356551667106568546291827001684869794402242067695854*i+1972744566958070881282131795626840370625118459932253321456562523309337576438614381897961997884583203821363249684189786452976563714388989414218292121069137192174721660268448964759287049) over Finite Field in i of size 2638940411073262671963620699288286770183560231187222316750407556465639836010558150163225530335162533481049256757217964651333810422125728537407397155806079217346919294449255613110157311^2
(1792805099210360888864761590321391235025824991548234912676247217808406536821234881384389175924130468280991088357660252370848305634037983159579204419296531735459329230669983096853856246*i + 171253309786548245036128932419221024429140017061733162803654587078736014845338272553757000723916403099300493601067652633948439740076865619503812837361164299530464912490228468097800783 : 354858932953470647164407208876248915819655125217303333206005726572045601374950018701435041440177841288062762055220650414072032960690957944114792835539535784706989279413982852603736575*i + 652241231208054817913369235175691302162155547428861981772486556413182925887029191547328926720048813218596706336154397071250972427384520853013935344373831652140490902941929446372831718 : 1)
(2186267301001259402114997355550578512125192708867710349339620240110565042023451739162302255305174185314466942521888744412961910909391429250064295777978302914701578195376147036042606489*i + 1113400569081370973415138408967328130898700595223023714237127216136706721906751381588571638690905466982759185164650150666678077272021890081392532363649111691002821924551541633624805969 : 475011489753746240024500178367364859418901588829939924748705578009262827369222834659815495729670558797454143390912073311509838111085236909370323483802926909195458815683174215323355088*i + 925039345882842856209794407096335244092780460386698951051338086161413597699668891541282650447520394073160493795142052782764553543711321165686302397695781016000953589530090195707014184 : 1)
"""

分析

一篇论文An Efficient Key Recovery Attack on SIDH

提出了一种针对超奇异异源性 Diffie-Hellman 协议（SIDH）的有效密钥恢复攻击。该攻击基于 Kani 对椭圆曲线乘积的等生性的“可还原性标准”，并强烈依赖于 Alice 和 Bob 在协议期间交换的扭点图像。如果我们假设知道起始曲线的自同态环，那么经典运行时间是输入大小的多项式（启发式），除了仅取决于系统参数的少量整数的因式分解。如果其中一方使用 2-isogenies，并且起始曲线配备了非常小程度的非标量自同态，那么攻击特别快速且易于实施

直接套板子

CastryckDecruAttack(E_start, P2, Q2, EB, PB, QB, two_i, num_cores=1)

题目中E_start, P2, Q2, EB, PB, QB, two_i都是已知的

from sage.all import ZZ, randint
from Crypto.Util.number import *
p = None

def generate_distortion_map(E):
    if E.a_invariants() != (0,6,0,1,0):
        raise NotImplementedError
    return E.isogeny(E.lift_x(ZZ(1)), codomain=E)

def generate_torsion_points(E, a, b):
    def get_l_torsion_basis(E, l):
        n = (p+1) // l
        return (n*G for G in E.gens())
    P2, Q2 = get_l_torsion_basis(E, 2**a)  # (3**b)*G1 ,G2
    P3, Q3 = get_l_torsion_basis(E, 3**b) # (2**a)*G1 , G2
    return P2, Q2, P3, Q3


def generate_key(E_start, b, P2, Q2, P3, Q3):
    bobs_key = flag
    K = P3 + bobs_key*Q3
    phi = E_start.isogeny(K, algorithm="factored")
    EB = phi.codomain()
    EB.set_order((p+1)**2, num_checks=0)
    PB, QB = phi(P2), phi(Q2)
    return bobs_key, EB, PB, QB


a = 305
b = 192
p = 2^a*3^b - 1
Fp2.<i> = GF(p^2, modulus=x^2+1)
R.<x> = PolynomialRing(Fp2)

E_start = EllipticCurve(Fp2, [0,6,0,1,0])
E_start.set_order((p+1)^2)

two_i = generate_distortion_map(E_start)

P2, Q2, P3, Q3 = generate_torsion_points(E_start, a, b)

PB = (1792805099210360888864761590321391235025824991548234912676247217808406536821234881384389175924130468280991088357660252370848305634037983159579204419296531735459329230669983096853856246*i + 171253309786548245036128932419221024429140017061733162803654587078736014845338272553757000723916403099300493601067652633948439740076865619503812837361164299530464912490228468097800783, 354858932953470647164407208876248915819655125217303333206005726572045601374950018701435041440177841288062762055220650414072032960690957944114792835539535784706989279413982852603736575*i + 652241231208054817913369235175691302162155547428861981772486556413182925887029191547328926720048813218596706336154397071250972427384520853013935344373831652140490902941929446372831718)
QB = (2186267301001259402114997355550578512125192708867710349339620240110565042023451739162302255305174185314466942521888744412961910909391429250064295777978302914701578195376147036042606489*i + 1113400569081370973415138408967328130898700595223023714237127216136706721906751381588571638690905466982759185164650150666678077272021890081392532363649111691002821924551541633624805969, 475011489753746240024500178367364859418901588829939924748705578009262827369222834659815495729670558797454143390912073311509838111085236909370323483802926909195458815683174215323355088*i + 925039345882842856209794407096335244092780460386698951051338086161413597699668891541282650447520394073160493795142052782764553543711321165686302397695781016000953589530090195707014184)

k1 = (1109655386602666580941477264844188509870568726343453010771770543665511250648180561681677488303290640863245633469198578301207900328491716466654470349910400724631139969542193124833051079*i+2116239248619087101677214169270633679594454755906693836568034229947351325062332338053907457802709748610111020509037164276717020111001082512633925347579357851693517057782645336434230575)
k2 =(783233241190388171387544682511032475647421068250023300290363249038620119995420899574317207343308349718411589404085433006020673690798356551667106568546291827001684869794402242067695854*i+1972744566958070881282131795626840370625118459932253321456562523309337576438614381897961997884583203821363249684189786452976563714388989414218292121069137192174721660268448964759287049)
load('castryck_decru_shortcut.sage')
EB = EllipticCurve(Fp2, [0,6,0,k1, k2])
EB.set_order((p+1)^2, num_checks=0)
PB=EB(PB)
QB=EB(QB)
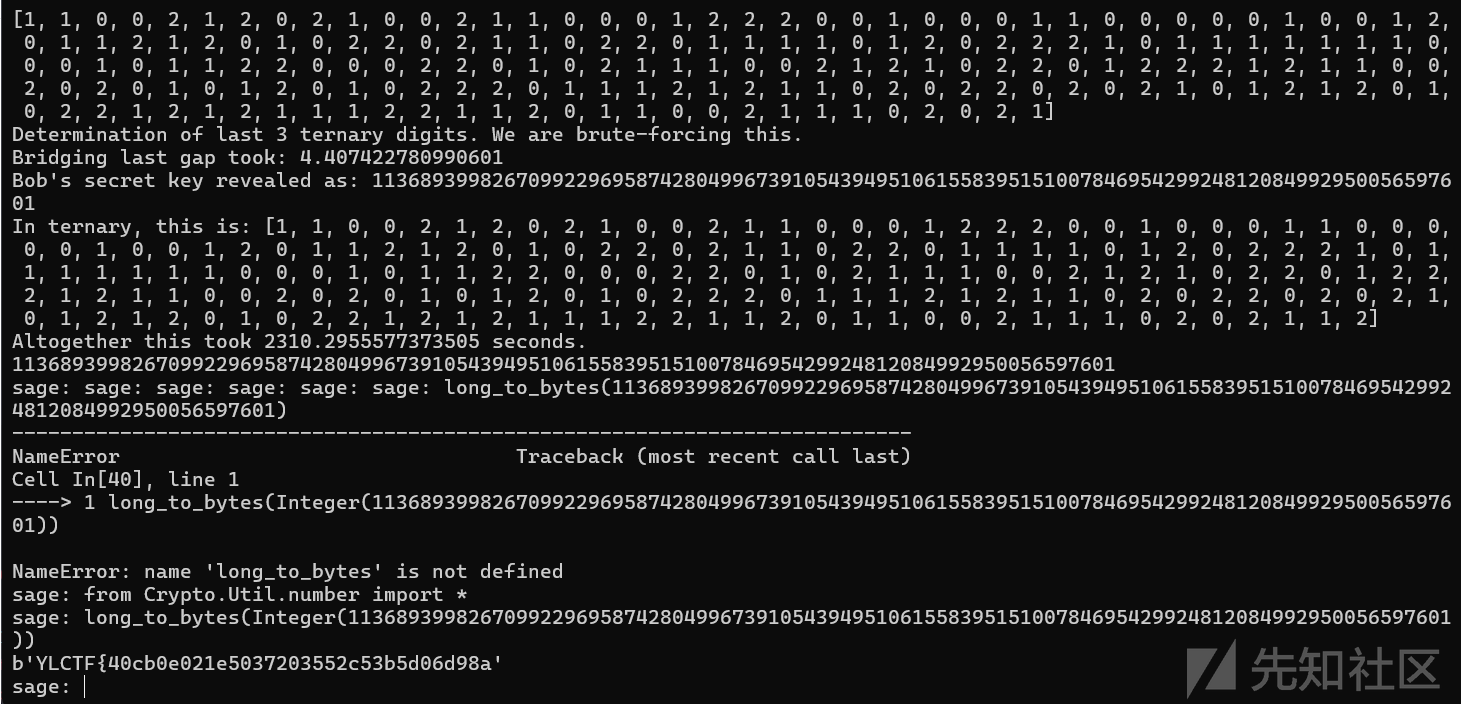
CastryckDecruAttack(E_start, P2, Q2, EB, PB, QB, two_i, num_cores=1)