2024网鼎杯青龙组-Crypto&Misc方向WP
Crypto
Crypto01
加密脚本:
from Crypto.Util.number import *
flag = b"***********************"
p = getPrime(512)
q = getPrime(512)
n = p * q
d = getPrime(299)
e = inverse(d, (p - 1) * (q - 1))
m = bytes_to_long(flag)
c = pow(m, e, n)
hint1 = p >> (512 - 70)
hint2 = q >> (512 - 70)
print(f"n = {n}")
print(f"e = {e}")
print(f"c = {c}")
print(f"hint1 = {hint1}")
print(f"hint2 = {hint2}")
论文题,需要参考Practical Attacks on Small Private Exponent

论文中提到,需要可以在一个低阶的的格上利用上高位的 Boneh-Durfee attack and Sarkar攻击,
借鉴大佬的脚本:
#sage
import time
time.clock = time.time
debug = True
strict = False
helpful_only = True
dimension_min = 7
def helpful_vectors(BB, modulus):
nothelpful = 0
for ii in range(BB.dimensions()[0]):
if BB[ii,ii] >= modulus:
nothelpful += 1
print (nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")
# 显示带有 0 和 X 的矩阵
def matrix_overview(BB, bound):
for ii in range(BB.dimensions()[0]):
a = ('%02d ' % ii)
for jj in range(BB.dimensions()[1]):
a += '0' if BB[ii,jj] == 0 else 'X'
if BB.dimensions()[0] < 60:
a += ' '
if BB[ii, ii] >= bound:
a += '~'
#print (a)
# 尝试删除无用的向量
def remove_unhelpful(BB, monomials, bound, current):
# 我们从当前 = n-1(最后一个向量)开始
if current == -1 or BB.dimensions()[0] <= dimension_min:
return BB
# 开始从后面检查
for ii in range(current, -1, -1):
# 如果它没有用
if BB[ii, ii] >= bound:
affected_vectors = 0
affected_vector_index = 0
# 让我们检查它是否影响其他向量
for jj in range(ii + 1, BB.dimensions()[0]):
# 如果另一个向量受到影响:
# 我们增加计数
if BB[jj, ii] != 0:
affected_vectors += 1
affected_vector_index = jj
# 如果没有其他载体最终受到影响
# 我们删除它
if affected_vectors == 0:
#print ("* removing unhelpful vector", ii)
BB = BB.delete_columns([ii])
BB = BB.delete_rows([ii])
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii-1)
return BB
#如果只有一个受到影响,我们会检查
# 如果它正在影响别的向量
elif affected_vectors == 1:
affected_deeper = True
for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
# 如果它影响哪怕一个向量
# 我们放弃这个
if BB[kk, affected_vector_index] != 0:
affected_deeper = False
# 如果没有其他向量受到影响,则将其删除,并且
# 这个有用的向量不够有用
#与我们无用的相比
if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):
#print ("* removing unhelpful vectors", ii, "and", affected_vector_index)
BB = BB.delete_columns([affected_vector_index, ii])
BB = BB.delete_rows([affected_vector_index, ii])
monomials.pop(affected_vector_index)
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii-1)
return BB
# nothing happened
return BB
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
"""
Boneh and Durfee revisited by Herrmann and May
在以下情况下找到解决方案:
* d < N^delta
* |x|< e^delta
* |y|< e^0.5
每当 delta < 1 - sqrt(2)/2 ~ 0.292
"""
# substitution (Herrman and May)
PR.<u, x, y> = PolynomialRing(ZZ) #多项式环
Q = PR.quotient(x*y + 1 - u) # u = xy + 1
polZ = Q(pol).lift()
UU = XX*YY + 1
# x-移位
gg = []
for kk in range(mm + 1):
for ii in range(mm - kk + 1):
xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kk
gg.append(xshift)
gg.sort()
# 单项式 x 移位列表
monomials = []
for polynomial in gg:
for monomial in polynomial.monomials(): #对于多项式中的单项式。单项式():
if monomial not in monomials: # 如果单项不在单项中
monomials.append(monomial)
monomials.sort()
# y-移位
for jj in range(1, tt + 1):
for kk in range(floor(mm/tt) * jj, mm + 1):
yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)
yshift = Q(yshift).lift()
gg.append(yshift) # substitution
# 单项式 y 移位列表
for jj in range(1, tt + 1):
for kk in range(floor(mm/tt) * jj, mm + 1):
monomials.append(u^kk * y^jj)
# 构造格 B
nn = len(monomials)
BB = Matrix(ZZ, nn)
for ii in range(nn):
BB[ii, 0] = gg[ii](0, 0, 0)
for jj in range(1, ii + 1):
if monomials[jj] in gg[ii].monomials():
BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)
#约化格的原型
if helpful_only:
# #自动删除
BB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)
# 重置维度
nn = BB.dimensions()[0]
if nn == 0:
print ("failure")
return 0,0
# 检查向量是否有帮助
if debug:
helpful_vectors(BB, modulus^mm)
# 检查行列式是否正确界定
det = BB.det()
bound = modulus^(mm*nn)
if det >= bound:
print ("We do not have det < bound. Solutions might not be found.")
print ("Try with highers m and t.")
if debug:
diff = (log(det) - log(bound)) / log(2)
print ("size det(L) - size e^(m*n) = ", floor(diff))
if strict:
return -1, -1
else:
print ("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")
# display the lattice basis
if debug:
matrix_overview(BB, modulus^mm)
# LLL
if debug:
print ("optimizing basis of the lattice via LLL, this can take a long time")
#BB = BB.BKZ(block_size=25)
BB = BB.LLL()
if debug:
print ("LLL is done!")
# 替换向量 i 和 j ->多项式 1 和 2
if debug:
print ("在格中寻找线性无关向量")
found_polynomials = False
for pol1_idx in range(nn - 1):
for pol2_idx in range(pol1_idx + 1, nn):
# 对于i and j, 构造两个多项式
PR.<w,z> = PolynomialRing(ZZ)
pol1 = pol2 = 0
for jj in range(nn):
pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)
pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)
# 结果
PR.<q> = PolynomialRing(ZZ)
rr = pol1.resultant(pol2)
if rr.is_zero() or rr.monomials() == [1]:
continue
else:
print ("found them, using vectors", pol1_idx, "and", pol2_idx)
found_polynomials = True
break
if found_polynomials:
break
if not found_polynomials:
print ("no independant vectors could be found. This should very rarely happen...")
return 0, 0
rr = rr(q, q)
# solutions
soly = rr.roots()
if len(soly) == 0:
print ("Your prediction (delta) is too small")
return 0, 0
soly = soly[0][0]
ss = pol1(q, soly)
solx = ss.roots()[0][0]
return solx, soly
def example():
############################################
# 随机生成数据
##########################################
#start_time =time.perf_counter
start =time.clock()
size=512
length_N = 2*size
ss=0
s=70
M=1 # the number of experiments
delta = 299/1024
# p = random_prime(2^512,2^511)
for i in range(M):
N =
e =
c =
hint1 = # p高位
hint2 = # q高位
# print ("p真实高",s,"比特:", int(p/2^(512-s)))
# print ("q真实高",s,"比特:", int(q/2^(512-s)))
# N = p*q;
# 解密指数d的指数( 最大0.292)
m = 7 # 格大小(越大越好/越慢)
t = round(((1-2*delta) * m)) # 来自 Herrmann 和 May 的优化
X = floor(N^delta) #
Y = floor(N^(1/2)/2^s) # 如果 p、 q 大小相同,则正确
for l in range(int(hint1),int(hint1)+1):
print('\n\n\n l=',l)
pM=l;
p0=pM*2^(size-s)+2^(size-s)-1;
q0=N/p0;
qM=int(q0/2^(size-s))
A = N + 1-pM*2^(size-s)-qM*2^(size-s);
#A = N+1
P.<x,y> = PolynomialRing(ZZ)
pol = 1 + x * (A + y) #构建的方程
# Checking bounds
#if debug:
#print ("=== 核对数据 ===")
#print ("* delta:", delta)
#print ("* delta < 0.292", delta < 0.292)
#print ("* size of e:", ceil(log(e)/log(2))) # e的bit数
# print ("* size of N:", len(bin(N))) # N的bit数
#print ("* size of N:", ceil(log(N)/log(2))) # N的bit数
#print ("* m:", m, ", t:", t)
# boneh_durfee
if debug:
##print ("=== running algorithm ===")
start_time = time.time()
solx, soly = boneh_durfee(pol, e, m, t, X, Y)
if solx > 0:
#print ("=== solution found ===")
if False:
print ("x:", solx)
print ("y:", soly)
d_sol = int(pol(solx, soly) / e)
ss=ss+1
print ("=== solution found ===")
print ("p的高比特为:",l)
print ("q的高比特为:",qM)
print ("d=",d_sol)
if debug:
print("=== %s seconds ===" % (time.time() - start_time))
#break
print("ss=",ss)
#end=time.process_time
end=time.clock()
print('Running time: %s Seconds'%(end-start))
if __name__ == "__main__":
example()
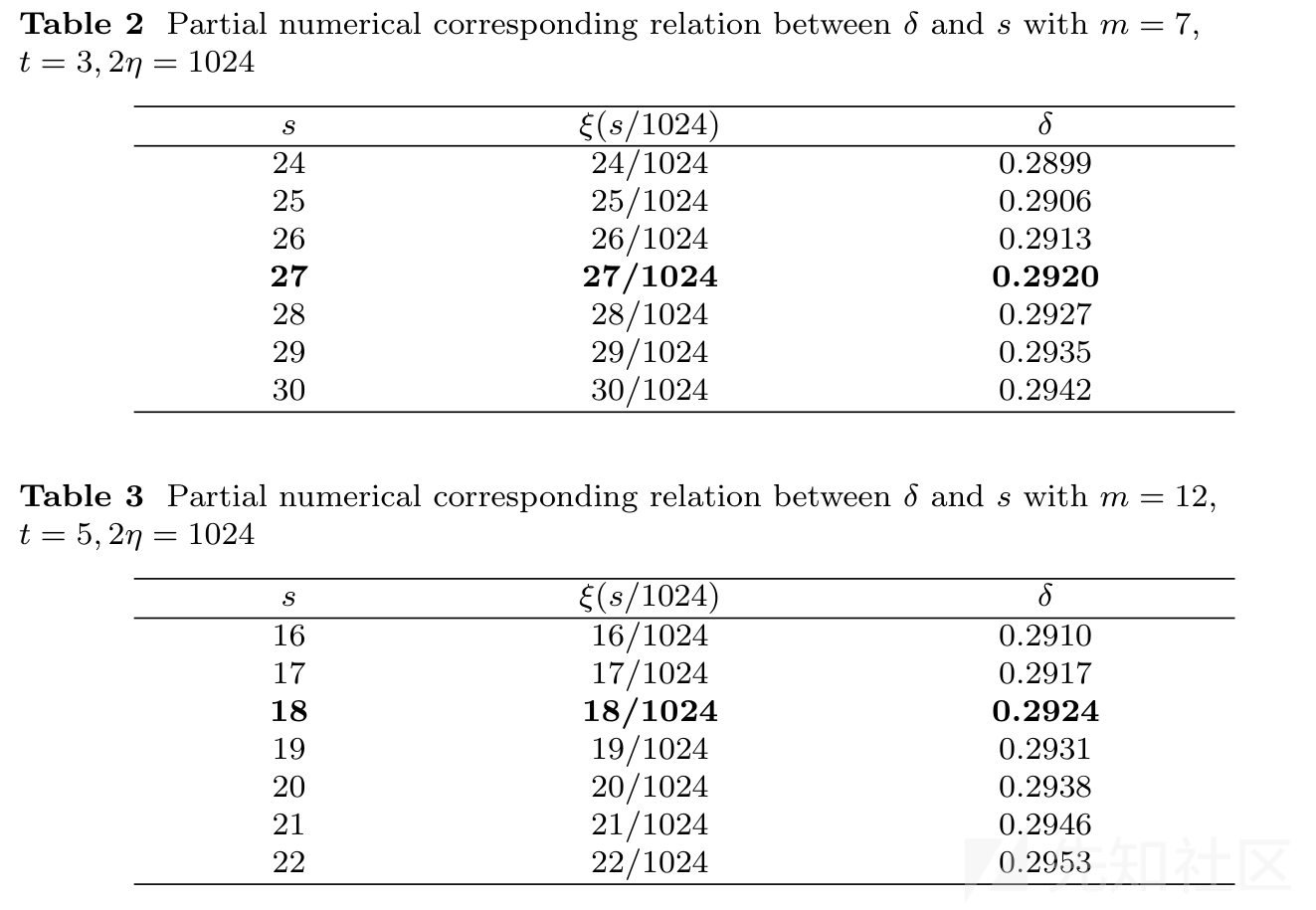
在这道题中,模数n为1024位,泄露的高位为70位,可以实施攻击,得到d,从而解出flag
Crypto02
加密脚本:
import gmpy2
import random
import binascii
from hashlib import sha256
from sympy import nextprime
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import long_to_bytes
from FLAG import flag
def victory_encrypt(plaintext, key):
key = key.upper()
key_length = len(key)
plaintext = plaintext.upper()
ciphertext = ""
for i, char in enumerate(plaintext):
if char.isalpha():
shift = ord(key[i % key_length]) - ord("A")
encrypted_char = chr((ord(char) - ord("A") + shift) % 26 + ord("A"))
ciphertext += encrypted_char
else:
ciphertext += char
return ciphertext
victory_key = "WANGDINGCUP"
victory_encrypted_flag = victory_encrypt(flag, victory_key)
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
a = 0
b = 7
xG = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
yG = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
G = (xG, yG)
n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
h = 1
zero = (0, 0)
dA = nextprime(random.randint(0, n))
if dA > n:
print("warning!!")
def addition(t1, t2):
if t1 == zero:
return t2
if t2 == zero:
return t2
(m1, n1) = t1
(m2, n2) = t2
if m1 == m2:
if n1 == 0 or n1 != n2:
return zero
else:
k = (3 * m1 * m1 + a) % p * gmpy2.invert(2 * n1, p) % p
else:
k = (n2 - n1 + p) % p * gmpy2.invert((m2 - m1 + p) % p, p) % p
m3 = (k * k % p - m1 - m2 + p * 2) % p
n3 = (k * (m1 - m3) % p - n1 + p) % p
return (int(m3), int(n3))
def multiplication(x, k):
ans = zero
t = 1
while t <= k:
if (k & t) > 0:
ans = addition(ans, x)
x = addition(x, x)
t <<= 1
return ans
def getrs(z, k):
(xp, yp) = P
r = xp
s = (z + r * dA % n) % n * gmpy2.invert(k, n) % n
return r, s
z1 = random.randint(0, p)
z2 = random.randint(0, p)
k = random.randint(0, n)
P = multiplication(G, k)
# hA = multiplication(G, dA)
r1, s1 = getrs(z1, k)
r2, s2 = getrs(z2, k)
print("r1 = {}".format(r1))
print("r2 = {}".format(r2))
print("s1 = {}".format(s1))
print("s2 = {}".format(s2))
print("z1 = {}".format(z1))
print("z2 = {}".format(z2))
key = sha256(long_to_bytes(dA)).digest()
cipher = AES.new(key, AES.MODE_CBC)
iv = cipher.iv
encrypted_flag = cipher.encrypt(pad(victory_encrypted_flag.encode(), AES.block_size))
encrypted_flag_hex = binascii.hexlify(iv + encrypted_flag).decode("utf-8")
print("Encrypted flag (AES in CBC mode, hex):", encrypted_flag_hex)
# output
# r1 = 28857061626266697731960297346547380130694223166851804642930502594650578288425
# r2 = 28857061626266697731960297346547380130694223166851804642930502594650578288425
# s1 = 81842916501936654327181596127464444170184582938148211467350979906270329843047
# s2 = 54199410087637342004207138894657653701426382978399616033659324046436549994669
# z1 = 114768147762808206397023700697633814229154932218327120646122869299219028759434
# z2 = 63513092260201266423877548128429517837199255134650637253201969399356248912467
# ('Encrypted flag (AES in CBC mode, hex):', u'51559ebae12fdd12e0e84df2baf07e3389b688398a71b62717fb77e0f6abdd40d848ee028b70681bc566ef2729d80b7a2778ad5b322b68501b6bbcef820b4719')
- 首先是一个字母表置换的加密,类似于维吉尼亚加密,并且密钥已知
- 然后使用了一个椭圆曲线进行了两次标量乘法(参数为曲线
secp256k1的参数),并且给出了很多结果 - 最后使用椭圆曲线的私钥,作为key对flag进行AES加密,模式为CBC,并且初始向量iv已知
仔细观察,给出了(r1,s1),(r2,s2)的情况下是可以建立两个方程解出私钥dA和k的,从而使用dA得到AES的key
import binascii
from hashlib import sha256
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
from Crypto.Util.number import *
def victory_decrypt(ciphertext, key):
key = key.upper()
key_length = len(key)
ciphertext = ciphertext.upper()
plaintext = ""
for i, char in enumerate(ciphertext):
if char.isalpha():
shift = ord(key[i % key_length]) - ord("A")
decrypted_char = chr((ord(char) - ord("A") - shift + 26) % 26 + ord("A"))
plaintext += decrypted_char
else:
plaintext += char
return plaintext
n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
r1 = r2 = px = (28857061626266697731960297346547380130694223166851804642930502594650578288425)
s1 = 81842916501936654327181596127464444170184582938148211467350979906270329843047
s2 = 54199410087637342004207138894657653701426382978399616033659324046436549994669
z1 = 114768147762808206397023700697633814229154932218327120646122869299219028759434
z2 = 63513092260201266423877548128429517837199255134650637253201969399356248912467
k = ((z1 - z2) * inverse(s1 - s2, n)) % n
dA = ((s1 * k - z1) * inverse(px, n)) % n
key = sha256(long_to_bytes(dA)).digest()
CC = "51559ebae12fdd12e0e84df2baf07e3389b688398a71b62717fb77e0f6abdd40d848ee028b70681bc566ef2729d80b7a2778ad5b322b68501b6bbcef820b4719"
iv = CC[:32]
iv = bytes.fromhex(iv)
cipher = AES.new(key, AES.MODE_CBC, iv)
flag = cipher.decrypt(binascii.unhexlify(CC[32:]))
flag = unpad(flag, 16).decode()
print(flag)
victory_key = "WANGDINGCUP"
flag = victory_decrypt(flag, victory_key)
print(flag.lower())
Misc
Misc03
流量题,在网站被攻击后分析攻击者的IP地址:
筛选http协议,首先发现一个IP在对网站信息目录扫描的操作:
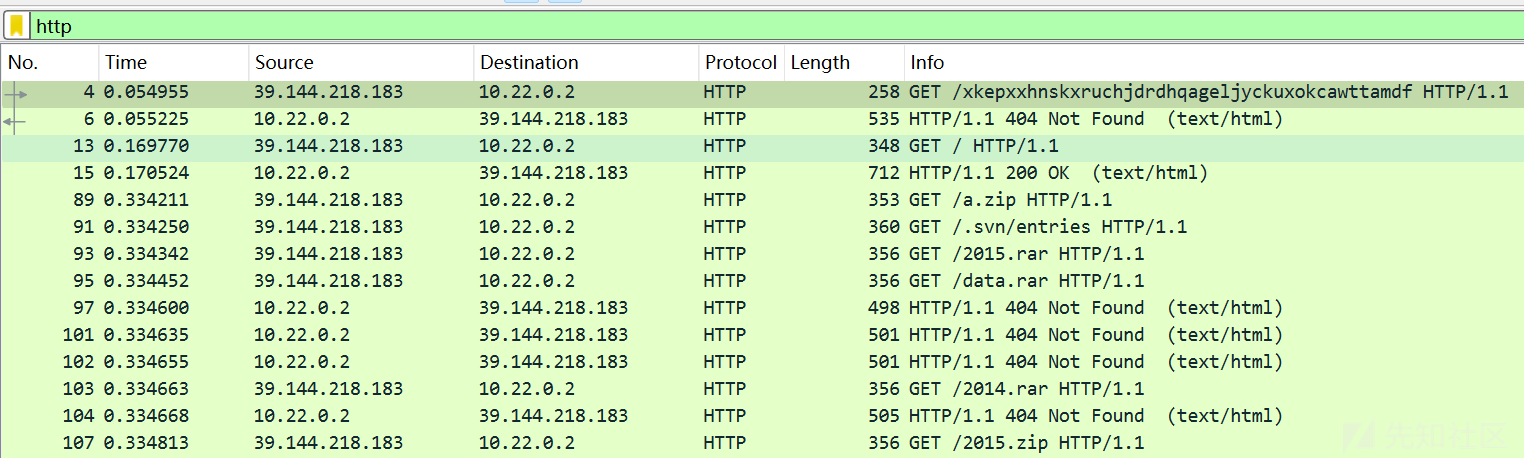
进一步筛选POST请求和200的相应:http.request.method=="POST" || http.response.code==200
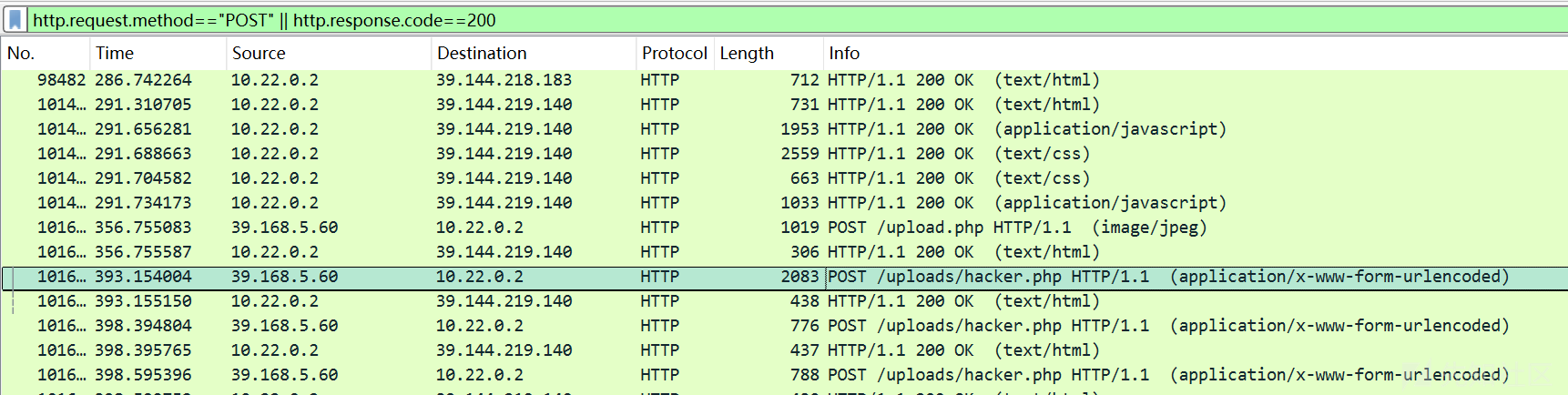
发现存在文件上传攻击,攻击者上传了一个hacker.php木马,

于是发现了攻击者的ip为 39.168.5.60
Misc04
图片加密,查看图片的相关信息,发现尺寸为729x729,大概率是二维码

图片似乎可以分割成一个个块的结构,似乎存在围绕中心的旋转
想到了一道皮亚诺分形曲线加密的题目,把脚本拿过来用,就能还原得到一张二维码:
于是,先把图片中存在的黑色污点去除,再使用皮亚诺曲线解密脚本:
from PIL import Image
from tqdm import tqdm
def peano(n):
if n == 0:
return [[0, 0]]
else:
in_lst = peano(n - 1)
lst = in_lst.copy()
px, py = lst[-1]
lst.extend([px - i[0], py + 1 + i[1]] for i in in_lst)
px, py = lst[-1]
lst.extend([px + i[0], py + 1 + i[1]] for i in in_lst)
px, py = lst[-1]
lst.extend([px + 1 + i[0], py - i[1]] for i in in_lst)
px, py = lst[-1]
lst.extend([px - i[0], py - 1 - i[1]] for i in in_lst)
px, py = lst[-1]
lst.extend([px + i[0], py - 1 - i[1]] for i in in_lst)
px, py = lst[-1]
lst.extend([px + 1 + i[0], py + i[1]] for i in in_lst)
px, py = lst[-1]
lst.extend([px - i[0], py + 1 + i[1]] for i in in_lst)
px, py = lst[-1]
lst.extend([px + i[0], py + 1 + i[1]] for i in in_lst)
return lst
def fix(img):
width, height = img.size
img_ = img.copy()
for i in range(1, width, 3):
for j in range(1, height, 3):
pixel = img.getpixel((i, j))
# 往附近8个方向填充
for x in range(-1, 2):
for y in range(-1, 2):
img_.putpixel((i + x, j + y), pixel)
return img_
order = peano(6)
img = Image.open(r"1.png")
width, height = img.size
block_width = width
block_height = height
img = fix(img)
new_image = Image.new("RGB", (width, height))
for i, (x, y) in tqdm(enumerate(order)):
new_x, new_y = i % width, i // width
pixel = img.getpixel((x, height - 1 - y))
new_image.putpixel((new_x, new_y), pixel)
new_image.save("new.png")
这时图片还不能直接识别,为了识别方便,需要先旋转到正确的方向,再转换成黑白的图片,编写一个脚本最终得到图片
from PIL import Image
import numpy as np
def rotate():
new_arr = np.rot90(img_arr, 1)
new_arr = np.rot90(new_arr, 1)
return new_arr
def color(img_arr):
for i in range(0, width):
for j in range(0, height):
if img_arr[i][j][0] == 0:
img_arr[i][j] = [255, 255, 255]
else:
img_arr[i][j] = [0, 0, 0]
new_img = Image.fromarray(img_arr)
new_img.save("new2.png")
img = Image.open("new.png")
width, height = img.size
img_arr = np.array(img)
color(rotate())

0 条评论
可输入 255 字


 转载
转载
 分享
分享
