网鼎杯-青龙组
crypto1
题目
# coding: utf-8
#!/usr/bin/env python2
import gmpy2
import random
import binascii
from hashlib import sha256
from sympy import nextprime
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import long_to_bytes
from FLAG import flag
#flag = 'wdflag{123}'
def victory_encrypt(plaintext, key):
key = key.upper()
key_length = len(key)
plaintext = plaintext.upper()
ciphertext = ''
for i, char in enumerate(plaintext):
if char.isalpha():
shift = ord(key[i % key_length]) - ord('A')
encrypted_char = chr((ord(char) - ord('A') + shift) % 26 + ord('A'))
ciphertext += encrypted_char
else:
ciphertext += char
return ciphertext
victory_key = "WANGDINGCUP"
victory_encrypted_flag = victory_encrypt(flag, victory_key)
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a = 0
b = 7
xG = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
yG = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
G = (xG, yG)
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
h = 1
zero = (0,0)
dA = nextprime(random.randint(0, n))
if dA > n:
print("warning!!")
def addition(t1, t2):
if t1 == zero:
return t2
if t2 == zero:
return t2
(m1, n1) = t1
(m2, n2) = t2
if m1 == m2:
if n1 == 0 or n1 != n2:
return zero
else:
k = (3 * m1 * m1 + a) % p * gmpy2.invert(2 * n1 , p) % p
else:
k = (n2 - n1 + p) % p * gmpy2.invert((m2 - m1 + p) % p, p) % p
m3 = (k * k % p - m1 - m2 + p * 2) % p
n3 = (k * (m1 - m3) % p - n1 + p) % p
return (int(m3),int(n3))
def multiplication(x, k):
ans = zero
t = 1
while(t <= k):
if (k &t )>0:
ans = addition(ans, x)
x = addition(x, x)
t <<= 1
return ans
def getrs(z, k):
(xp, yp) = P
r = xp
s = (z + r * dA % n) % n * gmpy2.invert(k, n) % n
return r,s
z1 = random.randint(0, p)
z2 = random.randint(0, p)
k = random.randint(0, n)
P = multiplication(G, k)
hA = multiplication(G, dA)
r1, s1 = getrs(z1, k)
r2, s2 = getrs(z2, k)
print("r1 = {}".format(r1))
print("r2 = {}".format(r2))
print("s1 = {}".format(s1))
print("s2 = {}".format(s2))
print("z1 = {}".format(z1))
print("z2 = {}".format(z2))
key = sha256(long_to_bytes(dA)).digest()
cipher = AES.new(key, AES.MODE_CBC)
iv = cipher.iv
encrypted_flag = cipher.encrypt(pad(victory_encrypted_flag.encode(), AES.block_size))
encrypted_flag_hex = binascii.hexlify(iv + encrypted_flag).decode('utf-8')
print("Encrypted flag (AES in CBC mode, hex):", encrypted_flag_hex)
# output
# r1 = 86806104739558095745988469033305523200538774705708894815836887970976487278764
# r2 = 86806104739558095745988469033305523200538774705708894815836887970976487278764
# s1 = 93400851884262731807098055393482657423555590196362184363643455285862566867372
# s2 = 58741027521216057788923508334695668250013849866589902683641825341545919891746
# z1 = 47591695289461307212638536234394543297527537576682980326526736956079807805586
# z2 = 97911075901954715147720917205165523174582665086645698292621371632896283314804
# ('Encrypted flag (AES in CBC mode, hex):', u'86cd24e2914c0c4d9b87bea34005a98bd8587d14cae71909b917679d3328304e7915e6ba4cad1096faa4a85bc52f8056d3f21ef09516be8a5160f1b338a6b936')
分析

import binascii
from hashlib import sha256
import gmpy2
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
from Crypto.Util.number import inverse, long_to_bytes
def victory_decrypt(ciphertext, key):
key = key.upper()
key_length = len(key)
plaintext = ''
for i, char in enumerate(ciphertext):
if char.isalpha(): # 仅对字母进行解密
shift = ord(key[i % key_length]) - ord('A')
# 对字母进行逆向移位,恢复原始字母
decrypted_char = chr((ord(char) - ord('A') - shift + 26) % 26 + ord('A'))
plaintext += decrypted_char
else:
plaintext += char # 非字母字符不处理
return plaintext
victory_key = "WANGDINGCUP"
# victory_encrypted_flag = victory_decrypt(flag, victory_key)
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a = 0
b = 7
xG = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
yG = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
G = (xG, yG)
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
h = 1
zero = (0,0)
r1 = 86806104739558095745988469033305523200538774705708894815836887970976487278764
r2 = 86806104739558095745988469033305523200538774705708894815836887970976487278764
s1 = 93400851884262731807098055393482657423555590196362184363643455285862566867372
s2 = 58741027521216057788923508334695668250013849866589902683641825341545919891746
z1 = 47591695289461307212638536234394543297527537576682980326526736956079807805586
z2 = 97911075901954715147720917205165523174582665086645698292621371632896283314804
encrypted_flag_hex="86cd24e2914c0c4d9b87bea34005a98bd8587d14cae71909b917679d3328304e7915e6ba4cad1096faa4a85bc52f8056d3f21ef09516be8a5160f1b338a6b936"
# 恢复k
k=(z1-z2)*inverse((s1-s2),n)
dA=((s1*k-z1)*inverse(r1,n))%n
print(dA)
key = sha256(long_to_bytes(dA)).digest()
cipher = AES.new(key, AES.MODE_CBC)
encrypted_data = binascii.unhexlify(encrypted_flag_hex)
print(encrypted_data)
iv, encrypted_flag = encrypted_data[:16], encrypted_data[16:]
cipher = AES.new(key, AES.MODE_CBC, iv)
decrypted_victory_flag = (cipher.decrypt(encrypted_flag), AES.block_size)
print(decrypted_victory_flag)
v_flag="SDSRDO{8G4966PGEI96H59430IE235FVUX341H1}"
flag=victory_decrypt(v_flag,victory_key)
print(flag)
#WDFLAG{8E4966CABA96F59430CB235DBFB341E1}
crypto2
题目
from Crypto.Util.number import *
from secret import flag
p = getPrime(512)
q = getPrime(512)
n = p * q
d = getPrime(299)
e = inverse(d,(p-1)*(q-1))
m = bytes_to_long(flag)
c = pow(m,e,n)
hint1 = p >> (512-70)
hint2 = q >> (512-70)
print(f"n = {n}")
print(f"e = {e}")
print(f"c = {c}")
print(f"hint1 = {hint1}")
print(f"hint2 = {hint2}")
n = 73787944575265560659337066998651559854008554735456318333076159883563615536562553619509791556832630227860528135540580555475313775587694656733939337337162684083504013096398383073623252469953554083296109377792508578226035938969407231689553680824348024184291021105154956244179599769690508760502010020180061720019
e = 29567393844922147731100606267534953994449203725806042726345753844983783164567752859600595704301680439820601788437000356006329166887506988972343037285018001864800437750191409728833296698465447150521119258782212680439802048101817052671603259114861564484544609221844909301043673563931709693327971992359139371227
c = 45450360465574139870481845301350579669043708378076876540990465420189044791001300484095663295849190297258585508686905534568744689506644183459090297899984297370341547866178062353877908003401151052692574668213473397829536065790283637478791675039086877921443504800597649778898977086137114431286134700385182325815
hint1 = 954676601865566077628
hint2 = 599256795156046227992
分析
一道原题,生成299位私钥d,给定p和q高70位求私钥d。
一般情况下若(1/3)N(1/4) < d < N0.292,可以选择boneh_durfee攻击。本题d刚好卡在界上,根据论文,m=7时,需要27位即可求出d,给了p和q高70位,求出d十分富裕。
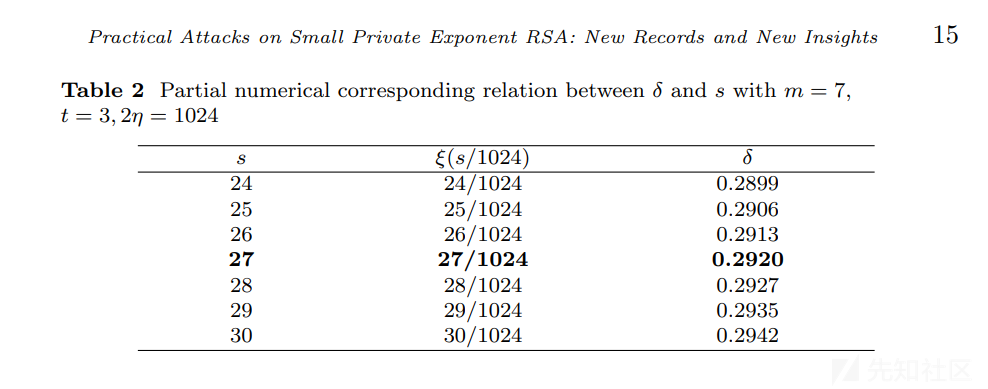
根据论文构造相应的Copper式子,修改代码。

在最初的代码上改动,即可求出d。
# 原代码
X = 2*floor(N^delta) # this _might_ be too much
Y = floor(N^(1/2)) # correct if p, q are ~ same size
P.<x,y> = PolynomialRing(ZZ)
A = int((N+1)/2)
pol = 1 + x * (A + y)
# 修改后
X = floor(N ^ delta) # this _might_ be too much
Y = floor(N ^ (1/2-70/1024)) # correct if p, q are ~ same size
P.<x,y> = PolynomialRing(ZZ)
A = int(N+1-(pm+qm)*2**(512-70))
pol = 1 + x * (A + y)
最终代码如下
from __future__ import print_function
import time
############################################
# Config
##########################################
"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = True
"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct
upperbound on the determinant. Note that this
doesn't necesseraly mean that no solutions
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False
"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7 # stop removing if lattice reaches that dimension
############################################
# Functions
##########################################
# display stats on helpful vectors
def helpful_vectors(BB, modulus):
nothelpful = 0
for ii in range(BB.dimensions()[0]):
if BB[ii, ii] >= modulus:
nothelpful += 1
print(nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")
# display matrix picture with 0 and X
def matrix_overview(BB, bound):
for ii in range(BB.dimensions()[0]):
a = ('%02d ' % ii)
for jj in range(BB.dimensions()[1]):
a += '0' if BB[ii, jj] == 0 else 'X'
if BB.dimensions()[0] < 60:
a += ' '
if BB[ii, ii] >= bound:
a += '~'
print(a)
# tries to remove unhelpful vectors
# we start at current = n-1 (last vector)
def remove_unhelpful(BB, monomials, bound, current):
# end of our recursive function
if current == -1 or BB.dimensions()[0] <= dimension_min:
return BB
# we start by checking from the end
for ii in range(current, -1, -1):
# if it is unhelpful:
if BB[ii, ii] >= bound:
affected_vectors = 0
affected_vector_index = 0
# let's check if it affects other vectors
for jj in range(ii + 1, BB.dimensions()[0]):
# if another vector is affected:
# we increase the count
if BB[jj, ii] != 0:
affected_vectors += 1
affected_vector_index = jj
# level:0
# if no other vectors end up affected
# we remove it
if affected_vectors == 0:
print("* removing unhelpful vector", ii)
BB = BB.delete_columns([ii])
BB = BB.delete_rows([ii])
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii - 1)
return BB
# level:1
# if just one was affected we check
# if it is affecting someone else
elif affected_vectors == 1:
affected_deeper = True
for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
# if it is affecting even one vector
# we give up on this one
if BB[kk, affected_vector_index] != 0:
affected_deeper = False
# remove both it if no other vector was affected and
# this helpful vector is not helpful enough
# compared to our unhelpful one
if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(
bound - BB[ii, ii]):
print("* removing unhelpful vectors", ii, "and", affected_vector_index)
BB = BB.delete_columns([affected_vector_index, ii])
BB = BB.delete_rows([affected_vector_index, ii])
monomials.pop(affected_vector_index)
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii - 1)
return BB
# nothing happened
return BB
"""
Returns:
* 0,0 if it fails
* -1,-1 if `strict=true`, and determinant doesn't bound
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
"""
Boneh and Durfee revisited by Herrmann and May
finds a solution if:
* d < N^delta
* |x| < e^delta
* |y| < e^0.5
whenever delta < 1 - sqrt(2)/2 ~ 0.292
"""
# substitution (Herrman and May)
PR.<u, x, y> = PolynomialRing(ZZ)
Q = PR.quotient(x * y + 1 - u) # u = xy + 1
polZ = Q(pol).lift()
UU = XX * YY + 1
# x-shifts
gg = []
for kk in range(mm + 1):
for ii in range(mm - kk + 1):
xshift = x ^ ii * modulus ^ (mm - kk) * polZ(u, x, y) ^ kk
gg.append(xshift)
gg.sort()
# x-shifts list of monomials
monomials = []
for polynomial in gg:
for monomial in polynomial.monomials():
if monomial not in monomials:
monomials.append(monomial)
monomials.sort()
# y-shifts (selected by Herrman and May)
for jj in range(1, tt + 1):
for kk in range(floor(mm / tt) * jj, mm + 1):
yshift = y ^ jj * polZ(u, x, y) ^ kk * modulus ^ (mm - kk)
yshift = Q(yshift).lift()
gg.append(yshift) # substitution
# y-shifts list of monomials
for jj in range(1, tt + 1):
for kk in range(floor(mm / tt) * jj, mm + 1):
monomials.append(u ^ kk * y ^ jj)
# construct lattice B
nn = len(monomials)
BB = Matrix(ZZ, nn)
for ii in range(nn):
BB[ii, 0] = gg[ii](0, 0, 0)
for jj in range(1, ii + 1):
if monomials[jj] in gg[ii].monomials():
BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU, XX, YY)
# Prototype to reduce the lattice
if helpful_only:
# automatically remove
BB = remove_unhelpful(BB, monomials, modulus ^ mm, nn - 1)
# reset dimension
nn = BB.dimensions()[0]
if nn == 0:
print("failure")
return 0, 0
# check if vectors are helpful
if debug:
helpful_vectors(BB, modulus ^ mm)
# check if determinant is correctly bounded
det = BB.det()
bound = modulus ^ (mm * nn)
if det >= bound:
print("We do not have det < bound. Solutions might not be found.")
print("Try with highers m and t.")
if debug:
diff = (log(det) - log(bound)) / log(2)
print("size det(L) - size e^(m*n) = ", floor(diff))
if strict:
return -1, -1
else:
print("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")
# display the lattice basis
if debug:
matrix_overview(BB, modulus ^ mm)
# LLL
if debug:
print("optimizing basis of the lattice via LLL, this can take a long time")
BB = BB.LLL()
if debug:
print("LLL is done!")
# transform vector i & j -> polynomials 1 & 2
if debug:
print("looking for independent vectors in the lattice")
found_polynomials = False
for pol1_idx in range(nn - 1):
for pol2_idx in range(pol1_idx + 1, nn):
# for i and j, create the two polynomials
PR.<w, z> = PolynomialRing(ZZ)
pol1 = pol2 = 0
for jj in range(nn):
pol1 += monomials[jj](w * z + 1, w, z) * BB[pol1_idx, jj] / monomials[jj](UU, XX, YY)
pol2 += monomials[jj](w * z + 1, w, z) * BB[pol2_idx, jj] / monomials[jj](UU, XX, YY)
# resultant
PR.<q> = PolynomialRing(ZZ)
rr = pol1.resultant(pol2)
# are these good polynomials?
if rr.is_zero() or rr.monomials() == [1]:
continue
else:
print("found them, using vectors", pol1_idx, "and", pol2_idx)
found_polynomials = True
break
if found_polynomials:
break
if not found_polynomials:
print("no independant vectors could be found. This should very rarely happen...")
return 0, 0
rr = rr(q, q)
# solutions
soly = rr.roots()
if len(soly) == 0:
print("Your prediction (delta) is too small")
return 0, 0
soly = soly[0][0]
ss = pol1(q, soly)
solx = ss.roots()[0][0]
#
return solx, soly
def example():
############################################
# How To Use This Script
##########################################
#
# The problem to solve (edit the following values)
#
# the modulus
N = 73787944575265560659337066998651559854008554735456318333076159883563615536562553619509791556832630227860528135540580555475313775587694656733939337337162684083504013096398383073623252469953554083296109377792508578226035938969407231689553680824348024184291021105154956244179599769690508760502010020180061720019
# the public exponent
e = 29567393844922147731100606267534953994449203725806042726345753844983783164567752859600595704301680439820601788437000356006329166887506988972343037285018001864800437750191409728833296698465447150521119258782212680439802048101817052671603259114861564484544609221844909301043673563931709693327971992359139371227
pm = 954676601865566077628
qm = 599256795156046227992
# the hypothesis on the private exponent (the theoretical maximum is 0.292)
delta = 299/1024 # this means that d < N^delta
#
# Lattice (tweak those values)
#
# you should tweak this (after a first run), (e.g. increment it until a solution is found)
m = 7 # size of the lattice (bigger the better/slower)
# you need to be a lattice master to tweak these
t = int((1 - 2 * delta) * m) # optimization from Herrmann and May
X = floor(N ^ delta) # this _might_ be too much
Y = floor(N ^ (1 / 2 - 70/1024)) # correct if p, q are ~ same size
#
# Don't touch anything below
#
# Problem put in equation
P.<x, y> = PolynomialRing(ZZ)
A = int(N + 1 - (pm + qm) * 2 ** (512 - 70))
pol = 1 + x * (A + y)
#
# Find the solutions!
#
# Checking bounds
if debug:
print("=== checking values ===")
print("* delta:", delta)
print("* delta < 0.292", delta < 0.292)
print("* size of e:", int(log(e) / log(2)))
print("* size of N:", int(log(N) / log(2)))
print("* m:", m, ", t:", t)
# boneh_durfee
if debug:
print("=== running algorithm ===")
start_time = time.time()
solx, soly = boneh_durfee(pol, e, m, t, X, Y)
# found a solution?
if solx > 0:
print("=== solution found ===")
if False:
print("x:", solx)
print("y:", soly)
d = int(pol(solx, soly) / e)
print("private key found:", d)
else:
print("=== no solution was found ===")
if debug:
print(("=== %s seconds ===" % (time.time() - start_time)))
return d
if __name__ == "__main__":
from Crypto.Util.number import long_to_bytes
d = example()
n = 73787944575265560659337066998651559854008554735456318333076159883563615536562553619509791556832630227860528135540580555475313775587694656733939337337162684083504013096398383073623252469953554083296109377792508578226035938969407231689553680824348024184291021105154956244179599769690508760502010020180061720019
c = 45450360465574139870481845301350579669043708378076876540990465420189044791001300484095663295849190297258585508686905534568744689506644183459090297899984297370341547866178062353877908003401151052692574668213473397829536065790283637478791675039086877921443504800597649778898977086137114431286134700385182325815
print(long_to_bytes(int(pow(c, d, n))))
网鼎杯 - 朱雀组
crypto2
题目
1)RSA模数 n:
0x00b8cb1cca99b6ac41876c18845732a5cbfc875df346ee9002ce608508b5fcf6b60a5ac7722a2d64ef74e1443a338e70a73e63a303f3ac9adf198595699f6e9f30c009d219c7d98c4ec84203610834029c79567efc08f66b4bc3f564bfb571546a06b7e48fb35bb9ccea9a2cd44349f829242078dfa64d525927bfd55d099c024f
(2)素数 p 的高位:
0xe700568ff506bd5892af92592125e06cbe9bd45dfeafe931a333c13463023d4f0000000000000000000000000000000000000000000000000000000000000000
(3)加密指数 e:
0x10001
(4)加密消息文件:flag.enc,你需要读取并解密此文件。
你的任务是通过给定的信息恢复素数 p,计算私钥 d,并解密加密消息以获得 flag。题解
n=1024bit ,p=512,这里已知p的高256bit,已知 p 的高位,那么可以分解出 p
当epsilon调至最小,即0.01时;p为512bit,p的高位至少泄露264bit时候,环多项式方程在模n情况下有解,但是现在只泄露了高256位,还需要爆破8bit才能copper出来(考的copper的临界问题)
from Crypto.Util.number import bytes_to_long, inverse, long_to_bytes
from tqdm import tqdm
# f = open("flag.enc","rb").read()
# c = bytes_to_long(f)
# print(c)
n=0x00b8cb1cca99b6ac41876c18845732a5cbfc875df346ee9002ce608508b5fcf6b60a5ac7722a2d64ef74e1443a338e70a73e63a303f3ac9adf198595699f6e9f30c009d219c7d98c4ec84203610834029c79567efc08f66b4bc3f564bfb571546a06b7e48fb35bb9ccea9a2cd44349f829242078dfa64d525927bfd55d099c024f
p_high=0xe700568ff506bd5892af92592125e06cbe9bd45dfeafe931a333c13463023d4f
c=23232542173220999599963005219461235233322210895267146367994372353935441385103369541932099361290797690653115070884377082654937605368499764138829158386382282355399879013292492149945145990813536892212037941497194332171531169746361299175556599056065926898531826815290696814472840679093485410835517411588039652443
e=0x10001
for i in tqdm(range(2**8,1,-1)):
ph = p_high<<8
ph = ph + i
kbits = 512 - 256-8
ph = ph << kbits
R.<x> = PolynomialRing(Zmod(n))
f = x + ph
x = f.small_roots(X=2^kbits, beta=0.4, epsilon=0.01)
if x:
p = ph + int(x[0])
if n%p==0:
print(p)
d=inverse(e,(p-1)*(n//p-1))
m=long_to_bytes(pow(c,int(d),n))
print(m)
crypto3
题目
#!/usr/bin/env python3
import random
from sympy import nextprime
from gmpy2 import is_prime
from Crypto.Util.number import getPrime, bytes_to_long
from Secret import flag
m = bytes_to_long(flag)
p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 2999
f = open("out.txt", 'w')
p1 = getPrime(1024)
q1 = nextprime(2024 * p1)
n1 = p1 * q1
f.write("n1 = {0}\n".format(n1))
p2 = getPrime(1024)
q2 = 1
while q2 < p2:
q2 = getPrime(1024)
n2 = p2 * q2
n22 = p2 * p2 + q2 * q2
f.write("n2 = {0}\n".format(n2))
f.write("n22 = {0}\n".format(n22))
r = random.getrandbits(1024)
p3 = r
while not is_prime(p3):
p3 += random.getrandbits(400)
q3 = r
while q3 < p3:
q3 += random.getrandbits(500)
while not is_prime(p3):
q3 += random.getrandbits(500)
n3 = p3 * q3
f.write("n3 = {0}\n".format(n3))
m1 = p1 * m * m + p2 * m + p3
m2 = q1 * m * m + q2 * m + q3
c1 = pow(m1, e, n)
c2 = pow(m2, e, n)
f.write("n = {0}\n".format(n))
f.write("c1 = {0}\n".format(c1))
f.write("c2 = {0}\n".format(c2))
题解

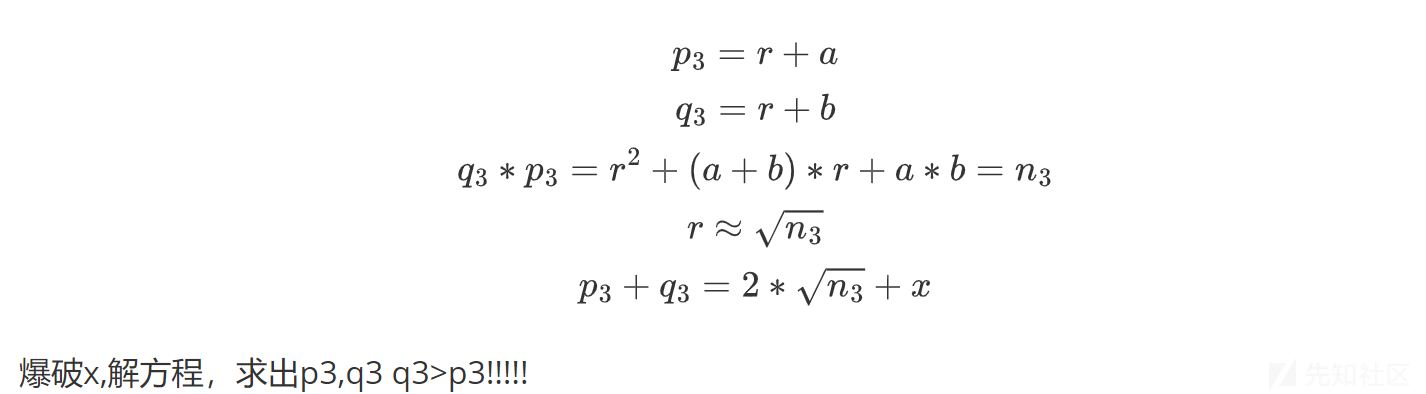
from Crypto.Util.number import long_to_bytes
from gmpy2 import gmpy2
from sympy import symbols, Eq,solve
from tqdm import tqdm
n1 = 49038077884252975192895442140098776691670772201751076509151354322881334047520804979429740882803123379351177623300782688308613625721402517963418527547300361816847273425082993791741129861551920174080993586984289910807626842342217366490597056078330511364252664108756229985040731917317552859532812073639281905439981113752840726776851958008225367884016530323513126274880806347377492293738939356177897280626798212418973765113580939065128111899664031434383620337048579049467460289658123235578775163077758914624762364934668565523617844590873896553769093078365975842295011810698806791445167392322829239575568839058942260833387349
n2 = 22202067802254662754415384555362780675819721336218458712498667628538691207127684848200512286167238639208810336197980264540632142880908586346658186262086562250409524188243332226071630184434785393109528371252795921300589634062803298555109381369217775593532055005855992147885536658170828170250750138914914904400776056919570440965685315340197406386852127615044132423796852306474686425560887845647623467731859387658813899356048837249443636758616154372185563083085906561486707794859441176889674247727076149663262997084214933848061196023027665175171682762546946900151004765425528825026552813191909586485560458395426718337251
n22 = 44636658891516560531590342003913220620507770919803045536985169630594025668750059868856255607462125755287255818878355953895763389469650524890033793326411499223618126326255906136738261127364579027624429095953245834076606803746489146108136302743814144566582052457811206500367547126181257741678383121087238175045812476930792219287833175749697900885000839080517709252022891462698481785288237679183837733999378756334961780844166676836723032283280786114254421382279987754394903805304822287087555778280845447058392816069557099568005651073581203043114433155712748630755553345366302273772484515986541549476418358558894904499402
n3 = 12928382931683267184171667528269368893431640073686336603181500456326185940136826698383827589126443262107901149453356579033699688565128005685439627826441006824820338067077017196868792110379452156330525710029302319090713579853598162183227456357362054680247101236874618555868171912770899671391522404982185287643292323817716113788068514149694362341126807278974390072669661968568894188544019148937014750662836050106093909704794181099589456584316360668413693088276999982261077933035060819741477135569463025009936687624163006709455967957492007566257447345630883416291873993510753930585443874467012846040141122710967882689774
n = 20460406765349534711456863755491813653852629264059673496458870668550687272318681610568303259207813490269883418212031965591371614344225538483485724393419427506325569341265050691869642273689168272003490296822826209687936035291801859796041951675482220249020431722168436216303886232192735072962945609269243891102114668581672305209147577550835535094104626953800321238592993265854533324230866209400770672759867502226881924677733913313507578554454291144430182827481897420134899577307688543867267558602843132221147647488931683114484495405062379895044634954699896775445005141349479843305859209080020297482228797911438762878567
c1 = 2739430692035971414352660686174180421920929725465552663578895784762501060590100291237661259759303279475320383734083549193310877194314192792679067468222206947806815628760443854315379317076503217321207666135074353647774546734541602630771365202520132694504545933844642623273649975730081012321213334370680290797985759307280929696883329863952608484502810192343845567595149590856457302565391337221919816005996471151632889914774260355024311771475447705363492241461074676671447624889435696912360783554758648270169677989746788093896374075202403894108238772515099651341223075356370693916256476141835762563612822287277802738952
c2 = 20378478408142806263314707665499572954493475371189994545364397367308211870461614448468159843167326957293019757944146580132729657886636900187680011606730204123020479169656791294424250229270250884868634070398364911846179697889692858857333386076560146644899632690164705628276452272416246074531607334006149583647914414459642054713181162811524058291613411690413927931104996581695174933499250878425396042376764292991929018264206036906890577888626395276884078460223062135176641332964869543360184737581525229619102035643668203046563588511278666026205719589351815495565902957308329952740324600754946068689907528249112378012984
e=2999
p1=gmpy2.iroot(n1//2024,2)[0]
# print(n1%p)
#0
q1=n1//p1
p2_add_q2=int(gmpy2.iroot(n22+2*n2,2)[0])
#sage
# var('p2 q2')
# f1=p2+q2-p2_add_q2
# f2=p2*q2-n2
# solve([f1==0,f2==0],[p2,q2])
p2 = 156822877987551658188094341746897451268581380333979857413461409363275297896982591266332128152404208821345349071302312613350787861803079248439802078645288934389875922882475942874739475473462838161583766136013916725645191333182111289415663968937506961590412047428988092475842796901767175311516254635625024912391
q2 = 141574163713645316061968537424205719189140127902050516111076795277546801688963726496904417705718089601559499107997753049403897075237213328581118415402604035046271696830602970021574519929640061042186789672209605939776673365717987957398377031406585132977708338425782662986975370522879274619125684784938928475461
assert p2*q2==n2
p3_add_q3=2*int(gmpy2.iroot(n3,2)[0])
p3, q3 = symbols('p3 q3')
# 定义方程
f2 = Eq(p3 * q3, n3)
for i in tqdm(range(0, 1000)):
f1 = Eq(p3 + q3 - p3_add_q3 - i, 0)
re = solve([f1, f2], [p3, q3])
# print(re)
if re:
# print(re)
p3=re[0][0]
q3=re[0][1]
print(p3)
print(q3)
break
assert p3*q3==n3
# print(q3>p3)
print(f'{p1=}')
print(f'{q1=}')
print(f'{p2=}')
print(f'{q2=}')
print(f'{p3=}')
print(f'{q3=}')

相关消息攻击,但是这里e=2999,而很大,要用HGCD(half gcd)加速多项式得gcd
from Crypto.Util.number import long_to_bytes
n = 20460406765349534711456863755491813653852629264059673496458870668550687272318681610568303259207813490269883418212031965591371614344225538483485724393419427506325569341265050691869642273689168272003490296822826209687936035291801859796041951675482220249020431722168436216303886232192735072962945609269243891102114668581672305209147577550835535094104626953800321238592993265854533324230866209400770672759867502226881924677733913313507578554454291144430182827481897420134899577307688543867267558602843132221147647488931683114484495405062379895044634954699896775445005141349479843305859209080020297482228797911438762878567
c1 = 2739430692035971414352660686174180421920929725465552663578895784762501060590100291237661259759303279475320383734083549193310877194314192792679067468222206947806815628760443854315379317076503217321207666135074353647774546734541602630771365202520132694504545933844642623273649975730081012321213334370680290797985759307280929696883329863952608484502810192343845567595149590856457302565391337221919816005996471151632889914774260355024311771475447705363492241461074676671447624889435696912360783554758648270169677989746788093896374075202403894108238772515099651341223075356370693916256476141835762563612822287277802738952
c2 = 20378478408142806263314707665499572954493475371189994545364397367308211870461614448468159843167326957293019757944146580132729657886636900187680011606730204123020479169656791294424250229270250884868634070398364911846179697889692858857333386076560146644899632690164705628276452272416246074531607334006149583647914414459642054713181162811524058291613411690413927931104996581695174933499250878425396042376764292991929018264206036906890577888626395276884078460223062135176641332964869543360184737581525229619102035643668203046563588511278666026205719589351815495565902957308329952740324600754946068689907528249112378012984
e=2999
p1=155654422840879658972839176671224183022703556222865008046143941427028196965990689093086532300927789178516570375637235131005691588261322281666566038503134894859072127189276590001780216632754422773137314564140171923526819538097120310925101377886723890953645237509999897694749001653029665105305616733360327518577
q1=315044551829940429761026493582557746437951997795078776285395337448305070659165154724407141377077845297317538440289763905155519774640916298093129661930345027194761985431095818163603158464694951692829924677819707973218282745108571509312405188842729155290177960720239792934171979345732042173138568268321302897600037
q2=156822877987551658188094341746897451268581380333979857413461409363275297896982591266332128152404208821345349071302312613350787861803079248439802078645288934389875922882475942874739475473462838161583766136013916725645191333182111289415663968937506961590412047428988092475842796901767175311516254635625024912391
p2=141574163713645316061968537424205719189140127902050516111076795277546801688963726496904417705718089601559499107997753049403897075237213328581118415402604035046271696830602970021574519929640061042186789672209605939776673365717987957398377031406585132977708338425782662986975370522879274619125684784938928475461
p3=113703047152146574229550275281898632632697999953298050573359502065285387983371913902739564070034443667693132915201789664886954096796775758264532519717054954348710881535125849152806750904950823486149865622633698196007298067246730750626265768593074777916707825236770445319057931652497714993260493836308910142191
q3=113703047152146574229550275281898632632697999953298050573359502065285387983371913902739564070034443667693132915201789664886954096796775758264532519717054954350084359920730210409867812288502365678046093981863957225263748387031314576411627659084852357331476260087648659843053338276110540078482599529469143280114
def HGCD(a, b):
if 2 * b.degree() <= a.degree() or a.degree() == 1:
return 1, 0, 0, 1
m = a.degree() // 2
a_top, a_bot = a.quo_rem(x ^ m)
b_top, b_bot = b.quo_rem(x ^ m)
R00, R01, R10, R11 = HGCD(a_top, b_top)
c = R00 * a + R01 * b
d = R10 * a + R11 * b
q, e = c.quo_rem(d)
d_top, d_bot = d.quo_rem(x ^ (m // 2))
e_top, e_bot = e.quo_rem(x ^ (m // 2))
S00, S01, S10, S11 = HGCD(d_top, e_top)
RET00 = S01 * R00 + (S00 - q * S01) * R10
RET01 = S01 * R01 + (S00 - q * S01) * R11
RET10 = S11 * R00 + (S10 - q * S11) * R10
RET11 = S11 * R01 + (S10 - q * S11) * R11
return RET00, RET01, RET10, RET11
def GCD(a, b):
print(a.degree(), b.degree())
q, r = a.quo_rem(b)
if r == 0:
return b
R00, R01, R10, R11 = HGCD(a, b)
c = R00 * a + R01 * b
d = R10 * a + R11 * b
if d == 0:
return c.monic()
q, r = c.quo_rem(d)
if r == 0:
return d
return GCD(d, r)
PR.<x>=PolynomialRing(Zmod(n))
# replace a,b,c,d
g1 = (p1 * x * x + p2 * x + p3)^e - c1
g2 = (q1 * x * x + q2 * x + q3)^e - c2
res=GCD(g1, g2)
m = -res.monic().coefficients()[0]
print(long_to_bytes(int(m)))
网鼎杯-白虎组
Crypto1
题目
from sage.all import *
from Crypto.Util.number import *
block_size = 64
rounds = 14
P_permutation = Permutations(list(range(block_size))).random_element()
inverse_P_permutation = [P_permutation.index(i) for i in range(block_size)]
MASK = 0b1110001001111001000110010000100010101111101100101110100001001001
IV = 7
b2i = lambda x: Integer(sum([x[i] * 2**i for i in range(len(x))]))
def pad(x):
padlen = block_size - len(x) % block_size
return x + bytes([padlen] * padlen)
def P(x):
bit_x = x.bits()
if len(bit_x) < block_size:
bit_x.extend([0] * (block_size - len(bit_x)))
bit_x = [bit_x[P_permutation[i]] for i in range(block_size)]
return b2i(bit_x)
def P_inv(x):
bit_x = x.bits()
if len(bit_x) < block_size:
bit_x.extend([0] * (block_size - len(bit_x)))
bit_x = [bit_x[inverse_P_permutation[i]] for i in range(block_size)]
return b2i(bit_x)
def S(x):
x1 = x
x2 = x << IV & MASK
x3 = x << IV & ((1 << block_size) - 1) | MASK
return x1 ^ x2 ^ x3
def encrypt(message_block, key):
ret = message_block
for i in range(rounds):
ret = P_inv(S(P(ret)) ^ key)
return ret
from secret import flag
from hashlib import md5
message = pad(flag)
message = [Integer(bytes_to_long(message[i:i+8])) for i in range(0, len(message), 8)]
key = int(md5(flag).hexdigest(), 16) & ((1 << block_size) - 1)
ciphertext = [encrypt(m, key) for m in message]
print(ciphertext)
print(P_permutation)
题解
整体来看这是一个分组加密算法,每8个字节一组,但是最少填充到64字节,看密文发现最后两组数据相同,说明这两段是被填充的,可以爆破pad填充的字节,从\x10起步。
加密在每轮中:
- P:首先对消息块进行置换。
- S:然后应用 S 函数进行替代。
- XOR:与密钥进行异或运算。
- P_inv:最后进行逆置换。
即进行了ret = P_inv(S(P(ret)) ^ key), P_inv和P函数互逆,最终结果可以看成ret = P_inv(S(S(S(S(...) ^ key) ^ key) ^ key) ^ key)
进行了14轮的S,可以使用Z3求解器解出可能的key。P_inv和P函数是根据序列置换每个比特的位置,无法简单直接的用Z3求解,所以选择化简表达式,只保留S这和比较简单的运算函数。
x = BitVec('x', block_size)
solver = Solver()
for i in range(rounds):
c0 = S(c0) ^ x
solver.add(c0 == P(kk))
if solver.check() == sat:
model = solver.model()
key = model[x].as_long()
c0表示第一轮的P(ret),我们这里的ret为爆破填充的8个字节。
kk为加密后最后一组数据,与明文填充的字节对应。
得出可能的key后可以直接解密了,这里我们还需要逆一下S函数,同样的使用Z3求解器,利用ai帮我们写一下S_inv。
最后写decrypt解密,与加密函数顺序相反即可。
需注意原题用sage,这里改用python,在P和P_inv中,bit_x = x.bits(),得到x的比特,在python中使用bin同样可以得到,但结果与sage相反(高低位相反),逆一下即可;Integer改为int。
from Crypto.Util.number import *
from z3 import *
block_size = 64
rounds = 14
P_permutation =
# P_permutation = Permutations(list(range(block_size))).random_element()
inverse_P_permutation = [P_permutation.index(i) for i in range(block_size)]
#
MASK = 0b1110001001111001000110010000100010101111101100101110100001001001
IV = 7
#
b2i = lambda x: int(sum([int(x[i] )* 2**i for i in range(len(x))]))
def pad(x):
padlen = block_size - len(x) % block_size
return x + bytes([padlen] * padlen)
def P(x):
# bit_x = x.bits()
bit_x = bin(x)[2:].zfill(block_size)[::-1]
if len(bit_x) < block_size:
bit_x.extend([0] * (block_size - len(bit_x)))
bit_x = [bit_x[P_permutation[i]] for i in range(block_size)]
return b2i(bit_x)
#
def P_inv(x):
# bit_x = x.bits()
bit_x = bin(x)[2:].zfill(block_size)[::-1]
if len(bit_x) < block_size:
bit_x.extend([0] * (block_size - len(bit_x)))
bit_x = [bit_x[inverse_P_permutation[i]] for i in range(block_size)]
return b2i(bit_x)
def S(x):
x1 = x
x2 = x << IV & MASK
x3 = x << IV & ((1 << block_size) - 1) | MASK
return x1 ^ x2 ^ x3
def S_inv(y):
# 创建一个 64 位的 BitVec 变量
x = BitVec('x', block_size)
# 创建一个求解器
solver = Solver()
# 定义 S 函数的约束
x1 = x
x2 = (x << IV) & BitVecVal(MASK, block_size)
x3 = (x << IV) & BitVecVal((1 << block_size) - 1, block_size) | BitVecVal(MASK, block_size)
constraint = x1 ^ x2 ^ x3 == BitVecVal(y, block_size)
# 添加约束
solver.add(constraint)
# 求解
if solver.check() == sat:
model = solver.model()
return model[x].as_long()
else:
raise ValueError("Inverse not found")
def encrypt(message_block, key):
ret = message_block
for i in range(rounds):
ret = P_inv(S(P(ret)) ^ key)
return ret
def decrypt(message_block, key):
ret = message_block
for i in range(rounds):
ret = P(ret)
ret = S_inv(ret ^ key)
ret = P_inv(ret)
return ret
c =
ppad = [bytes([i] * 8) for i in range(16, 64)]
kk = c[-1]
for p in ppad:
x = BitVec('x', block_size)
solver = Solver()
c0 = bytes_to_long(p)
c0 = P(c0)
for i in range(rounds):
c0 = S(c0) ^ x
solver.add(c0 == P(kk))
if solver.check() == sat:
model = solver.model()
key = model[x].as_long()
print(b"".join([long_to_bytes(decrypt(l, key)) for l in c]))
Crypto2
题目
from Crypto.Util.number import getPrime, isPrime, GCD, inverse
nbits = 2048
gbits = 1000
g = getPrime(int(gbits))
while True:
a = getPrime(int(nbits*0.5)-gbits)
p = 2*g*a + 1
if isPrime(p):
break
while True:
b = getPrime(int(nbits*0.5)-gbits)
q = 2*g*b + 1
if p!=q and isPrime(q):
break
N = p*q
e = 65537
def str2int(s):
return int(s.encode('latin-1').hex(),16)
def int2str(i):
tmp=hex(i)[2:]
if len(tmp)%2==1:
tmp='0'+tmp
return bytes.fromhex(tmp).decode('latin-1')
with open('pubkey.txt','w') as f:
f.write(str(e)+'\n')
f.write(str(N)+'\n')
with open('flag.txt') as f:
plain = str2int(f.read())
c = pow(plain,e,N)
with open('cipher.txt','wb') as f:
f.write(int2str(c).encode('latin-1'))
题解
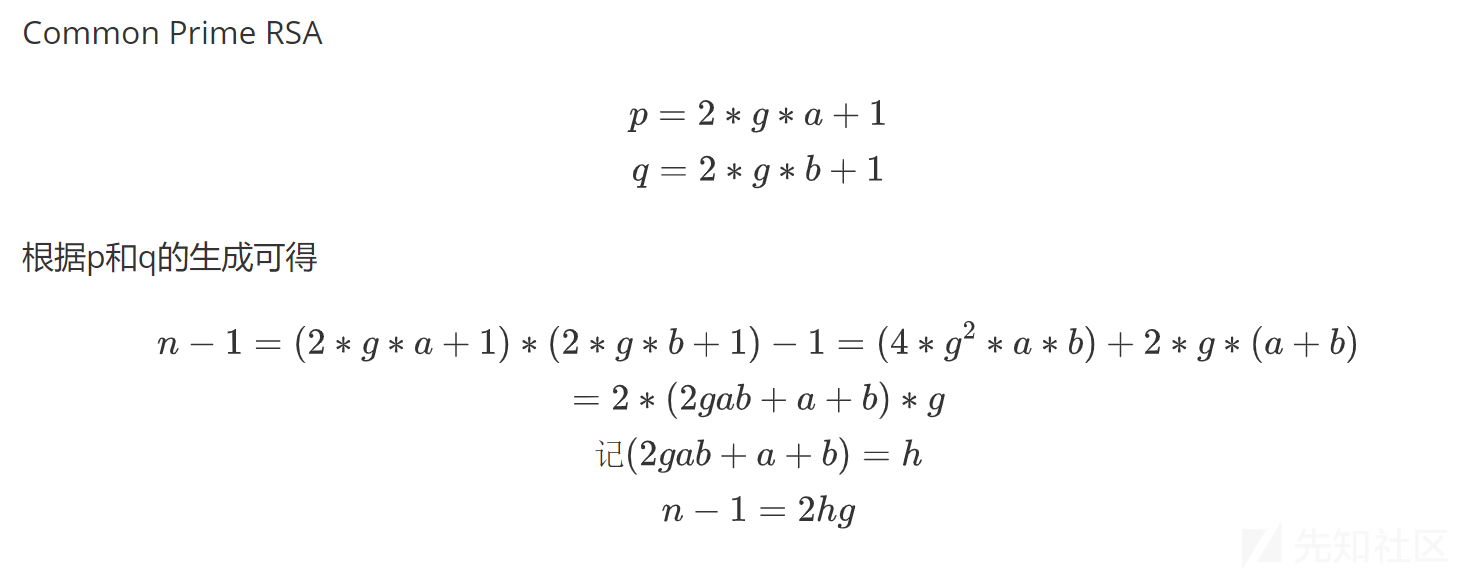
定义 γ 表示共因子 g 的相对于 N 的大小,即 g=N^γ。考虑 g≤N^(1/2),故 0≤γ≤1/2。
根据题目,nbit=2048,gbit=1000
γ约等于0.49,很接近1/2
当 γ 接近于 1/2 时,由于共素数RSA的特殊构造,我们可以在有限时间分解 N,算法时间复杂度接近于 O(1)。
只需修改 Pollard's rho method 的 xi 函数。
在 Mckee&Pinch 的论文中指出将 f(x)=x^2+1 修改为 f(x)=x^(N−1)+3(modN) 是最优解。

由于 N−1=2gh 且 p−1=2ga,故最多只有一个值不在 x^(N−1)modp 的环中。
所以再看见p-1和q-1的最大公约数非常大时,可以利用pollard rho来分解N
直接跑rho脚本
Common Prime RSA 笔记 | 独奏の小屋 (hasegawaazusa.github.io)
import gmpy2,sympy
from Crypto.Util.number import *
def f(x, n):
return (pow(x, n - 1, n) + 3) % n
def rho(n):
i = 1
while True:
a = getRandomRange(2, n)
b = f(a, n)
j = 1
while True:
p = GCD(abs(a - b), n)
print('{} in {} circle'.format(j, i))
if p == n:
break
elif p > 1:
return (p, n // p)
else:
a = f(a, n)
b = f(f(b, n), n)
j += 1
i += 1
n =
e = 65537
c = open("cipher.txt", "rb").read()
p, q = rho(n)
d = gmpy2.invert(e,(p-1)*(q-1))
print(long_to_bytes(pow(bytes_to_long(c), d, n)))

 转载
转载
 分享
分享

没有评论