文章 - CTF 中的 LFSR

线性反馈移位寄存器（LFSR）在流密码中有广泛的应用，是指给定前一状态的输出，将该输出的线性函数再用作输入的移位寄存器。LFSR 主要用于生成一串随机的比特流，比特流可用做加密明文的密钥。

LFSR 基本原理大致就是通过当前状态进行一些线性运算来确定下一状态。不清楚的可以参考这篇文章学习一下流密码和 LFSR 。

最开始接触 LFSR 是在强网杯的 streamgame，后来密码学课程上比较详细学习了流密码和 LFSR，再到今年国赛初赛中的 oldstream，最近的 X-MAS CTF 中一道密码题我看到了 LFSR 的一些新玩法，总结一下。

2018 强网杯 streamgame1

看一下题目：

from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==25

def lfsr(R,mask):
    output = (R << 1) & 0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)



R=int(flag[5:-1],2)
mask    =   0b1010011000100011100

f=open("key","ab")
for i in range(12):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

可以发现 flag 是 19 位比特流，作为 LFSR 的初始状态，生成了 96 个比特并写入了 key 中。这里 2**19 时间复杂度并不大，直接采用暴力枚举的方式，脚本：

def lfsr(R,mask):
    output = (R << 1) & 0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)

key=[85,56,247,66,193,13,178,199,237,224,36,58]
mask=0b1010011000100011100

for k in range(2**19):
    R=k;
    a=''
    judge=1
    for i in range(12):
        tmp = 0
        for j in range(8):
            (k, out) = lfsr(k, mask)
            tmp = (tmp << 1) ^ out
        if(key[i]!=tmp):
           judge=0
           break
    if(judge==1):
        print 'flag{'+bin(R)[2:]+'}'
        break

结果：

flag{1110101100001101011}

2018 国赛 oldstreamgame

看一下题目：

flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14

def lfsr(R,mask):
    output = (R << 1) & 0xffffffff
    i=(R&mask)&0xffffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)

R=int(flag[5:-1],16)
mask = 0b10100100000010000000100010010100

f=open("key","w")
for i in range(100):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()python

同样是一个 LFSR，与之前不同的是 flag 是 8 位十六进制，也就是 LFSR 初始状态是 32 bit，这里我们也可以采用暴力枚举的方式，但是更好的方式是分析一下原理。

分析

我们仔细分析一下 lfsr 这个函数的作用：

函数传入 R 和 mask 两个参数，output 由 R 左移一位然后和 0xffffffff 进行了与操作得到，相当于把原来 R 的最高比特位顶掉了，末尾填了一个 0 。i 是由 R 和 mask 进行了与操作，后面的循环主要用于得到 lastbit。

lastbit 首先为 0，然后 lastbit 和 i &1 的结果异或，i 右移一位，以此类推，知道 i 为 0，不难分析出 lastbit 实际就是 i 的每个比特位异或得到的。在循环结束后 output 和 lastbit 进行了异或，由于之前 output 的最低比特是 0，所以相当于把 output 的最低位设成了 lastbit。函数返回 output 和 lastbit 返回。

总结一下 lfsr 这个函数：

对于传入的 R 和 mask，R 左移一位把最高位顶掉，最低一位由 R & mask 结果的各个比特位异或的结果进行填充。并返回最终结果和最低位。

可以看到这就是一个典型的线性反馈移位寄存器的实现，初始状态是 flag 的 32 比特位，随后不断顶掉高位，在最后一位填充。可以想象成一个长度为 32 的队列，每一次队列向前移动，最前面（最高位）的出去，后面填充的由前一状态的 32 个比特经过运算决定（具体就是 lastbit 的生成方法）。

我们看一下 lastbit 的生成方法，R 和 mask 进行与操作，mask 是 0b10100100000010000000100010010100,和 0 进行与操作肯定是 0，所以实际上 R 只有几个比特位起作用，就是 mask 为 1 的那些 bit 位。也就是说 R 的这些位异或得到了 lastbit。

这个 LFSR 当生成了第一个比特时，flag 最初始的 32 比特最高比特被顶出去了，生成第二个比特时，原始状态的第二高位被顶出去了。我们不妨想一下当生成第 32 个比特结束后，此时的状态就是 flag 最初始的 32 比特完全都被顶出去了。而这 32 个比特我们都已知（程序每次都把 lastbit 记录写进了 key 中）。此时状态的 32 个比特的最低位是由上一状态的 32 比特起作用的那些位异或得到的，而 mask 的最高位是 1，所以也就是上一个状态的最高位参与了异或运算，而上一个状态最高位就是被顶出去的 flag 初始状态的最低一位，此外我们可以得到参与异或运算的其他比特位，那么我们就可以算出初始状态的最低位了。

用式子来说明，把开始生成第 32 比特的状态比作 x，x[i] 代表从高到低的第几位，那么：

lastbit = x[1] ^ x[3] ^ x[6] ^ x[13] ^ x[21] ^ x[25] ^ x[28] ^ x[30]

lastbit 代表生成的第 32 个比特，x[1] 代表初始状态的最低比特位，这个式子中只有 x[1] 未知，我们可以计算出 x[1],这样我们就可以通过生成第 32 个比特后的状态还原了生成第 31 个比特后（生成第 32 个比特前）的状态，以此类推，经过 32 次我们可以完全还原到初始状态。

原理简单来说就是新生成的比特是通过上一个状态的特定比特异或得到，我们可以利用异或性质用生成的比特去还原原来的比特。

exp

根据思路写出解题脚本：

# -*- coding: utf-8 -*-
import libnum

def LFSR_inv(R,mask):
    str=bin(R)[2:].zfill(32)
    new=str[-1:]+str[:-1]
    new=int(new,2)                    #R循环右移一位得到new
    i = (new & mask) & 0xffffffff
    lastbit = 0
    while i != 0:
        lastbit ^= (i & 1)
        i = i >> 1
    return R>>1 | lastbit<<31         #最高位用lastbit填充

mask = 0b10100100000010000000100010010100
data=open('key').read()
data=data[:4]
c=libnum.s2n(data)                    #生成32比特后的状态
for _ in range(32):
    c=LFSR_inv(c,mask)
print hex(c)

运行得到结果：0x926201d7L

所以 flag 是

flag{926201d7}

2018 X-MAS CTF goodies

这个题算是一个 LFSR 的变形，感觉考的很有趣。看下题：

import os

flag = open('flag.txt').read().strip()


class PRNG():
    def __init__(self):
        self.seed = self.getseed()
        self.iv = int(bin(self.seed)[2:].zfill(64)[0:32], 2)
        self.key = int(bin(self.seed)[2:].zfill(64)[32:64], 2)
        self.mask = int(bin(self.seed)[2:].zfill(64)[64:96], 2)
        self.aux = 0

    def parity(self, x):
        x ^= x >> 16
        x ^= x >> 8
        x ^= x >> 4
        x ^= x >> 2
        x ^= x >> 1
        return x & 1

    def getseed(self):
        return int(os.urandom(12).encode('hex'), 16)

    def LFSR(self):
        return self.iv >> 1 | (self.parity(self.iv & self.key) << 32)

    def next(self):
        self.aux, self.iv = self.iv, self.LFSR()

    def next_byte(self):
        x = self.iv ^ self.mask
        self.next()
        x ^= x >> 16
        x ^= x >> 8
        return (x & 255)


def encrypt(s):
    o = ''
    for x in s:
        o += chr(ord(x) ^ p.next_byte())
    return o.encode('hex')


p = PRNG()

with open('flag.enc', 'w') as f:
    f.write(encrypt(flag))

flag.enc:

ab38abdef046216128f8ea76ccfcd38a4a8649802e95f817a2fc945dc04a966d502ef1e31d0a2d

分析

可以看到程序采用异或方式加密了 flag，而每次与 flag 异或的字节由类中的 next_byte方法生成。我们再看一下这个类，发现构造函数初始化了四个变量，其中 iv、key、mask都是根据随机字符串生成的 32 位比特流，我们无法得知，aux 这个变量初始化为 0。

我们来从头过一下 next_byte这个方法是怎么生成一个字节的：

把 iv 和 mask 进行异或得到 x，进行 x ^= x >> 16 x ^= x >> 8 这两步，把 x & 255结果返回，这就是生成的字节。而在这之中调用了 next 方法改变了类的 iv，而 mask 始终不变。

我们不难发现这几步操作：

x ^= x >> 16
x ^= x >> 8
return x & 255

其实就是把 x 的低 32 bit 按顺序分成四组，每组 8 个比特，四组数进行异或就是返回的结果。（不信可以拿个数试试）

我们再来看一下 iv 每次是如何改变的，next 函数就一行语句：

self.aux, self.iv = self.iv, self.LFSR()

aux我们不管，因为它没有参与任何运算。新的 iv 被 LFSR 函数的返回值赋值，看一下 LFSR 函数：

return self.iv >> 1 | (self.parity(self.iv & self.key) << 32)

返回了 iv 与 parity 函数返回值右移 32 位进行或运算的结果。

我们再来看一下 parity 函数：

x ^= x >> 16
x ^= x >> 8
x ^= x >> 4
x ^= x >> 2
x ^= x >> 1
return x & 1

和前面 next_byte 的差不多，不难分析出这个 parity 实际就是把 x 的低 32 个比特之间进行异或，返回结果。当然，结果只能是 0 或1。

如果把 (self.parity(self.iv & self.key) << 32) 的结果比作 s，那么 s 两种可能，0 和 2**32。

新的 iv 是由当前的 iv 右移一位和 s 进行与操作得到的。注意这里 iv 可能是 32 位，也可能是 33 位，因为 2**32 是 33 位。

把各个函数和 iv 生成方法过了一遍，发现我们什么也不知道，已知只有密文，初始 iv ，mask，key 都是未知。但是还有一个条件，我们是知道 flag 是以X-MAS{开头的。这样我们可以得到 next_byte 生成的前 6 个字节，但是我们也无法还原初始 iv 和 mask，key。注意，我们只需要还原明文就可以了，不需要知道 iv，mask以及 key 。

我用一个图来说明一下字节的生成：

	i[1]	i[2]	i[3]	i[4]	i[5]	i[6]	i[7]	i[8]
xor	i[9]	i[10]	i[11]	i[12]	i[13]	i[14]	i[15]	i[16]
xor	i[17]	i[18]	i[19]	i[20]	i[21]	i[22]	i[23]	i[24]
xor	i[25]	i[26]	i[27]	i[28]	i[29]	i[30]	i[31]	i[32]
xor	m[1]	m[2]	m[3]	m[4]	m[5]	m[6]	m[7]	m[8]
xor	m[9]	m[10]	m[11]	m[12]	m[13]	m[14]	m[15]	m[16]
xor	m[17]	m[18]	m[19]	m[20]	m[21]	m[22]	m[23]	m[24]
xor	m[25]	m[26]	m[27]	m[28]	m[29]	m[30]	m[31]	m[32]

把 xor 当成正常的加法，一列的进行异或，最终得到的八个比特就是生成的字节。其中 i[1] 代表 iv 低32比特中从高到低的第 1 个比特（因为后面 iv 可能 33 个比特），m[5] 代表 mask 从高到低的第 5 个比特。

当下一次生成字节的时候，iv 因为发生了变化，变化后的 iv_new[2]—iv_new[32] 这 31 位是之前 iv[1]—iv[31] 这31 位（因为右移了一位），而 iv_new[1]是 0，可能新的 iv 有 33 位，但那个最高位并没有参与到字节的生成中，我们不需要管。此时生成字节的图是：

	0	i[1]	i[2]	i[3]	i[4]	i[5]	i[6]	i[7]
xor	i[8]	i[9]	i[10]	i[11]	i[12]	i[13]	i[14]	i[15]
xor	i[16]	i[17]	i[18]	i[19]	i[20]	i[21]	i[22]	i[23]
xor	i[24]	i[25]	i[26]	i[27]	i[28]	i[29]	i[30]	i[31]
xor	m[1]	m[2]	m[3]	m[4]	m[5]	m[6]	m[7]	m[8]
xor	m[9]	m[10]	m[11]	m[12]	m[13]	m[14]	m[15]	m[16]
xor	m[17]	m[18]	m[19]	m[20]	m[21]	m[22]	m[23]	m[24]
xor	m[25]	m[26]	m[27]	m[28]	m[29]	m[30]	m[31]	m[32]

这个图中的 i[1] 和上一个图中的 i[1] 表示的含义完全相同，就是初始的 iv 低32比特中从高到低的第一个比特。

我们可以发现，前四行异或的结果，和上一个图中前四行异或的结果，有 7 位都是相同的，相当于结果右移了一位，在前面又补了一位。但是 mask 和 iv 的异或对应关系被打乱了。

我们可以换一种思路想，虽然我们不知道 mask 的具体 32 个比特，但是有用的只有八个比特，就是后四行异或的结果。所以我们通过已知的六个字符明文X-MAS{和完整密文来算出这八个比特。至于前四行异或的结果，相当于一个 LFSR，右移一位，同时前面补位。

验证

我们有了明文的前六个字符X-MAS{以及密文，可以得到生成的前 6 个字节，我们来验证一下前面分析的是否正确。

c=open("flag.enc").read().decode("hex")
print len(c[6:])
byte=[]
flag="X-MAS{"
for i in range(6):
    byte.append(ord(c[i])^ord(flag[i]))
print byte
for i in range(256):
    if bin(byte[0]^i)[2:].zfill(8)[:7]==bin(byte[1]^i)[2:].zfill(8)[-7:]:
        print i,bin(byte[0]^i)[2:].zfill(8),bin(byte[1]^i)[2:].zfill(8)

运行发现输出：

[243, 21, 230, 159, 163, 61]
72 10111011 01011101
183 01000100 10100010

程序里的 i 就是表格中后面 4 行异或的结果，是两个... 我们再调整一下，把判断条件里的 byte[0] 和 byte[1] 改成byte[1] 和 byte[2]，看看结果一样不：

c=open("flag.enc").read().decode("hex")
byte=[]
flag="X-MAS{"
for i in range(6):
    byte.append(ord(c[i])^ord(flag[i]))
print byte                                  #生成的字节
for i in range(256):
    if bin(byte[1]^i)[2:].zfill(8)[:7]==bin(byte[2]^i)[2:].zfill(8)[-7:]:
        print i,bin(byte[1]^i)[2:].zfill(8),bin(byte[2]^i)[2:].zfill(8)

输出：

[243, 21, 230, 159, 163, 61]
72 01011101 10101110
183 10100010 01010001

也是 72 和183 ，验证了我们之前的分析时正确的。

这样我们解题思路就清晰了，得到了实际有用的 “mask”,我们只需要每次移位的时候，最高位填 0 和 1 都试一下，看看哪个解密能得到正常的字符。然后填充正确的比特，循环得到全部 flag。

exp

我们需要得到生成第 6 个字节后的状态：

c=open("flag.enc").read().decode("hex")
byte=[]
flag="X-MAS{"
for i in range(6):
    byte.append(ord(c[i])^ord(flag[i]))
print byte                                  #生成的字节
for i in range(256):
    if bin(byte[4]^i)[2:].zfill(8)[:7]==bin(byte[5]^i)[2:].zfill(8)[-7:]:
        print i,bin(byte[4]^i)[2:].zfill(8),bin(byte[5]^i)[2:].zfill(8)

输出：

[243, 21, 230, 159, 163, 61]
72 11101011 01110101
183 00010100 10001010

如果选用 72 作为有效 mask，此时状态是 01110101

写出 exp:

# -*- coding: utf-8 -*-
#written by R1sker

import string
list=string.ascii_letters+string.digits+"_"+"}"

def LFSR1(iv):
    return iv >> 1 | (1 << 7)
def LFSR0(iv):
    return iv >> 1 | (0 << 7)

c=open("flag.enc").read().decode("hex")
flag="X-MAS{"

mask=72
s=0b01110101
for j in c[6:]:
    if chr(ord(j)^mask^LFSR1(s)) in list:
        s=LFSR1(s)
        flag+=chr(ord(j)^mask^s)
        print flag
    elif chr(ord(j)^mask^LFSR0(s)) in list:
        s=LFSR0(s)
        flag += chr(ord(j) ^ mask ^ s)
        print flag

结果：

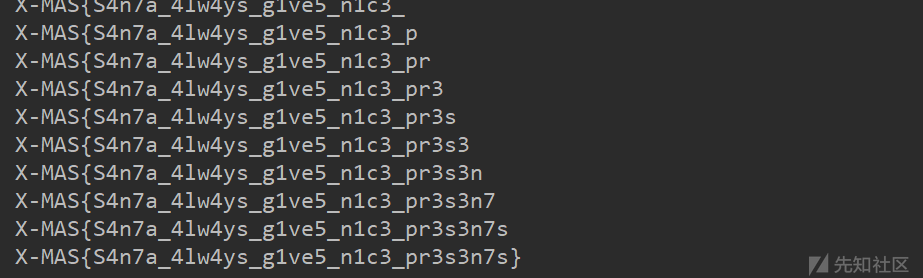
X-MAS{S4n7a_4lw4ys_g1ve5_n1c3_pr3s3n7s}

总结

Crypto 真好玩，滚去学 Web 了，毕竟还是一只 Web 狗。