文章 - 区块链安全—随机数安全分析（下）

一、前言

在上文中，我们主要是针对随机数安全进行了理论方面的密码学研究。在理论层面上我们又进行了简单代码的分析。而本文不在过多的介绍理论知识，而更多的将重点放在代码层面，针对现实实例中的代码进行安全分析。

二、比特币随机种子生成详解

首先我们来研究下区块链最大的应用——比特币在随机数方面是如何实现的。

首先我们将源码下载到本地，对random.h进行查看。得到源码：

/* Seed OpenSSL PRNG with additional entropy data */
void RandAddSeed();
/**
 * Functions to gather random data via the OpenSSL PRNG
 */
void GetRandBytes(unsigned char* buf, int num);
uint64_t GetRand(uint64_t nMax);
int GetRandInt(int nMax);
uint256 GetRandHash();

void RandAddSeedSleep();

/**
 * Function to gather random data from multiple sources, failing whenever any
 * of those source fail to provide a result.
 */
void GetStrongRandBytes(unsigned char* buf, int num);

/** Get 32 bytes of system entropy. Do not use this in application code: use
 * GetStrongRandBytes instead.
 */
void GetOSRand(unsigned char *ent32);

/** Check that OS randomness is available and returning the requested number
 * of bytes.
 */
bool Random_SanityCheck();

/** Initialize the RNG. */
void RandomInit();

我们对这些函数进行分析：

第一个函数void RandAddSeed();：通过OpenSSL的伪随机数发生器生成随机数种子。

void GetRandBytes(unsigned char* buf, int num)为通过OpenSSL的伪随机数发生器生成随机数据。

uint64_t GetRand(uint64_t nMax)为对生成的随机数进行获取。

int GetRandInt(int nMax)用于获取整数随机数。

uint256 GetRandHash()用于获取随机数哈希。

void RandAddSeedSleep()设置随机数生成的休眠时间。

void GetStrongRandBytes(unsigned char* buf, int num)从多个源进行随机数获取。

void GetOSRand(unsigned char *ent32)从操作系统底层获取随机数。

bool Random_SanityCheck()用于检查操作系统随机数是否可用。

void RandomInit()对伪随机数发生器进行初始化。

下面我们详细讲解下其中的部分函数功能：

首先我们可以看：

void RandAddSeed()
{
    // Seed with CPU performance counter
    int64_t nCounter = GetPerformanceCounter();
    RAND_add(&nCounter, sizeof(nCounter), 1.5);
    memory_cleanse((void*)&nCounter, sizeof(nCounter));
}

其中包含了三句话：
首先函数会获取硬件的时间戳，并将时间戳赋值给nCounter。之后调用了RAND_add函数以时间戳为种子生成了随机数。最后执行了内存清理函数。

而区块链还可以利用用户本地的操作系统数据进行随机数的生成：

我们来看GetOSRand(unsigned char *ent32)方法：

/** Get 32 bytes of system entropy. */
void GetOSRand(unsigned char *ent32)
{
#if defined(WIN32)
    HCRYPTPROV hProvider;
    int ret = CryptAcquireContextW(&hProvider, nullptr, nullptr, PROV_RSA_FULL, CRYPT_VERIFYCONTEXT);
    if (!ret) {
        RandFailure();
    }
    ret = CryptGenRandom(hProvider, NUM_OS_RANDOM_BYTES, ent32);
    if (!ret) {
        RandFailure();
    }
    CryptReleaseContext(hProvider, 0);
#elif defined(HAVE_SYS_GETRANDOM)
    /* Linux. From the getrandom(2) man page:
     * "If the urandom source has been initialized, reads of up to 256 bytes
     * will always return as many bytes as requested and will not be
     * interrupted by signals."
     */
    int rv = syscall(SYS_getrandom, ent32, NUM_OS_RANDOM_BYTES, 0);
    if (rv != NUM_OS_RANDOM_BYTES) {
        if (rv < 0 && errno == ENOSYS) {
            /* Fallback for kernel <3.17: the return value will be -1 and errno
             * ENOSYS if the syscall is not available, in that case fall back
             * to /dev/urandom.
             */
            GetDevURandom(ent32);
        } else {
            RandFailure();
        }
    }
#elif defined(HAVE_GETENTROPY) && defined(__OpenBSD__)
    /* On OpenBSD this can return up to 256 bytes of entropy, will return an
     * error if more are requested.
     * The call cannot return less than the requested number of bytes.
       getentropy is explicitly limited to openbsd here, as a similar (but not
       the same) function may exist on other platforms via glibc.
     */
    if (getentropy(ent32, NUM_OS_RANDOM_BYTES) != 0) {
        RandFailure();
    }
#elif defined(HAVE_GETENTROPY_RAND) && defined(MAC_OSX)
    // We need a fallback for OSX < 10.12
    if (&getentropy != nullptr) {
        if (getentropy(ent32, NUM_OS_RANDOM_BYTES) != 0) {
            RandFailure();
        }
    } else {
        GetDevURandom(ent32);
    }
#elif defined(HAVE_SYSCTL_ARND)
    /* FreeBSD and similar. It is possible for the call to return less
     * bytes than requested, so need to read in a loop.
     */
    static const int name[2] = {CTL_KERN, KERN_ARND};
    int have = 0;
    do {
        size_t len = NUM_OS_RANDOM_BYTES - have;
        if (sysctl(name, ARRAYLEN(name), ent32 + have, &len, nullptr, 0) != 0) {
            RandFailure();
        }
        have += len;
    } while (have < NUM_OS_RANDOM_BYTES);
#else
    /* Fall back to /dev/urandom if there is no specific method implemented to
     * get system entropy for this OS.
     */
    GetDevURandom(ent32);
#endif
}

在这些函数中会根据系统宏定义来判断是否为Windows32位系统并根据系统内置的函数提供者并配合随机函数生成随机数。若系统为Linux系统，则函数使用urandom来获取对应字节的随机数。如果系统为macOSX系统，那么系统会使用urandom生成随机数。

三、实例项目随机数漏洞

首先我们要讲解的实例是前段日子很火的以太坊Dice2win项目。

智能合约原理就是是借助EVM运行，跑在区块链上的合约代码。其最大的特点就是公开和不可篡改性。由于数据链上的信息可以被所有人（包括黑客）发现，所以如何在合约上生成随机数就成了一个大问题。

在我们所知道的Fomo3D合约中，我们发现在空投奖励的随机数生成中就引入了block信息作为随机数种子生成的参数，导致随机数种子只受到合约地址影响，无法做到完全随机。

代码如下：

function airdrop()
    private 
    view 
    returns(bool)
{
    uint256 seed = uint256(keccak256(abi.encodePacked(
        (block.timestamp).add
        (block.difficulty).add
        ((uint256(keccak256(abi.encodePacked(block.coinbase)))) / (now)).add
        (block.gaslimit).add
        ((uint256(keccak256(abi.encodePacked(msg.sender)))) / (now)).add
        (block.number)
    )));
    if((seed - ((seed / 1000) * 1000)) < airDropTracker_)
        return(true);
    else
        return(false);
}

在这个实例中，我们能够解读出此函数中定义了随机数种子。而此种子使用了区块链上所有用户均可见的参数：block.timestamp、block.difficulty、block.coinbase、block.gaslimit、block.number。而由于这些生成seed的参数只与msg.sender这一个变量相关，所以在Fome3D这个实例中出现了大量的薅羊毛事件，损失也是巨大的。

而对于此类问题如何应对呢？在Dice2win实例中提供了一个比较合理的随机数生成方式hash-commit-reveal，即玩家提交行动计划，然后行动计划hash后提交给后端，后端生成相应的hash值，然后生成对应的随机数reveal，返回对应随机数commit。这样，服务端拿不到行动计划，客户端也拿不到随机数。

function placeBet(uint betMask, uint modulo, uint commitLastBlock, uint commit, bytes32 r, bytes32 s) external payable {
        // Check that the bet is in 'clean' state.
        Bet storage bet = bets[commit];
        require (bet.gambler == address(0), "Bet should be in a 'clean' state.");

        // Validate input data ranges.
        uint amount = msg.value;
        require (modulo > 1 && modulo <= MAX_MODULO, "Modulo should be within range.");
        require (amount >= MIN_BET && amount <= MAX_AMOUNT, "Amount should be within range.");
        require (betMask > 0 && betMask < MAX_BET_MASK, "Mask should be within range.");

        // Check that commit is valid - it has not expired and its signature is valid.
        require (block.number <= commitLastBlock, "Commit has expired.");
        bytes32 signatureHash = keccak256(abi.encodePacked(uint40(commitLastBlock), commit));
        require (secretSigner == ecrecover(signatureHash, 27, r, s), "ECDSA signature is not valid.");

        uint rollUnder;
        uint mask;

        if (modulo <= MAX_MASK_MODULO) {
            // Small modulo games specify bet outcomes via bit mask.
            // rollUnder is a number of 1 bits in this mask (population count).
            // This magic looking formula is an efficient way to compute population
            // count on EVM for numbers below 2**40. For detailed proof consult
            // the dice2.win whitepaper.
            rollUnder = ((betMask * POPCNT_MULT) & POPCNT_MASK) % POPCNT_MODULO;
            mask = betMask;
        } else {
            // Larger modulos specify the right edge of half-open interval of
            // winning bet outcomes.
            require (betMask > 0 && betMask <= modulo, "High modulo range, betMask larger than modulo.");
            rollUnder = betMask;
        }

        // Winning amount and jackpot increase.
        uint possibleWinAmount;
        uint jackpotFee;

        (possibleWinAmount, jackpotFee) = getDiceWinAmount(amount, modulo, rollUnder);

        // Enforce max profit limit.
        require (possibleWinAmount <= amount + maxProfit, "maxProfit limit violation.");

        // Lock funds.
        lockedInBets += uint128(possibleWinAmount);
        jackpotSize += uint128(jackpotFee);

        // Check whether contract has enough funds to process this bet.
        require (jackpotSize + lockedInBets <= address(this).balance, "Cannot afford to lose this bet.");

        // Record commit in logs.
        emit Commit(commit);

        // Store bet parameters on blockchain.
        bet.amount = amount;
        bet.modulo = uint8(modulo);
        bet.rollUnder = uint8(rollUnder);
        bet.placeBlockNumber = uint40(block.number);
        bet.mask = uint40(mask);
        bet.gambler = msg.sender;
    }

    // This is the method used to settle 99% of bets. To process a bet with a specific
    // "commit", settleBet should supply a "reveal" number that would Keccak256-hash to
    // "commit". "blockHash" is the block hash of placeBet block as seen by croupier; it
    // is additionally asserted to prevent changing the bet outcomes on Ethereum reorgs.
    function settleBet(uint reveal, bytes32 blockHash) external onlyCroupier {
        uint commit = uint(keccak256(abi.encodePacked(reveal)));

        Bet storage bet = bets[commit];
        uint placeBlockNumber = bet.placeBlockNumber;

        // Check that bet has not expired yet (see comment to BET_EXPIRATION_BLOCKS).
        require (block.number > placeBlockNumber, "settleBet in the same block as placeBet, or before.");
        require (block.number <= placeBlockNumber + BET_EXPIRATION_BLOCKS, "Blockhash can't be queried by EVM.");
        require (blockhash(placeBlockNumber) == blockHash);

        // Settle bet using reveal and blockHash as entropy sources.
        settleBetCommon(bet, reveal, blockHash);
    }

在这个代码中，主要函数为placeBet和settleBet，其中placeBet函数主要为建立赌博，而settleBet为开奖。而在此合约中，我们完全遵守了hash-commit-reveal方案，随机数的实现放在了服务端，过程如下：

用户首先在项目平台中选择好自己需要下注的方式，之后点击确认下注。
之后服务端生成随机数reveal，生成本次赌博的随机数hash信息，有效最大blockNumber，并将这些数据进行签名，并将commit和信息签名传给用户。
用户将上述由随机数而得到的hash以及lastBlockNumber信息打包，并传入placebet函数。
服务端在一段时间之后，将带有随机数和服务端执行settlebet开奖，而此时开奖信息则可控，即选择部分对自己不利的中止，以使庄家获得更大的利润。

下面我们再看一个实例：

pragma solidity ^0.4.16;

contract Ethraffle_v4b {
    struct Contestant {
        address addr;
        uint raffleId;
    }

    event RaffleResult(
        uint raffleId,
        uint winningNumber,
        address winningAddress,
        address seed1,
        address seed2,
        uint seed3,
        bytes32 randHash
    );

    event TicketPurchase(
        uint raffleId,
        address contestant,
        uint number
    );

    event TicketRefund(
        uint raffleId,
        address contestant,
        uint number
    );


    function chooseWinner() private {
        address seed1 = contestants[uint(block.coinbase) % totalTickets].addr;
        address seed2 = contestants[uint(msg.sender) % totalTickets].addr;
        uint seed3 = block.difficulty;
        bytes32 randHash = keccak256(seed1, seed2, seed3);

        uint winningNumber = uint(randHash) % totalTickets;
        address winningAddress = contestants[winningNumber].addr;
        RaffleResult(raffleId, winningNumber, winningAddress, seed1, seed2, seed3, randHash);

        // Start next raffle
        raffleId++;
        nextTicket = 0;
        blockNumber = block.number;

        // gaps.length = 0 isn't necessary here,
        // because buyTickets() eventually clears
        // the gaps array in the loop itself.

        // Distribute prize and fee
        winningAddress.transfer(prize);
        feeAddress.transfer(fee);
    }

    // Get your money back before the raffle occurs
    function getRefund() public {
        uint refund = 0;
        for (uint i = 0; i < totalTickets; i++) {
            if (msg.sender == contestants[i].addr && raffleId == contestants[i].raffleId) {
                refund += pricePerTicket;
                contestants[i] = Contestant(address(0), 0);
                gaps.push(i);
                TicketRefund(raffleId, msg.sender, i);
            }
        }

        if (refund > 0) {
            msg.sender.transfer(refund);
        }
    }

    // Refund everyone's money, start a new raffle, then pause it
    function endRaffle() public {
        if (msg.sender == feeAddress) {
            paused = true;

            for (uint i = 0; i < totalTickets; i++) {
                if (raffleId == contestants[i].raffleId) {
                    TicketRefund(raffleId, contestants[i].addr, i);
                    contestants[i].addr.transfer(pricePerTicket);
                }
            }

            RaffleResult(raffleId, totalTickets, address(0), address(0), address(0), 0, 0);
            raffleId++;
            nextTicket = 0;
            blockNumber = block.number;
            gaps.length = 0;
        }
    }

    function togglePause() public {
        if (msg.sender == feeAddress) {
            paused = !paused;
        }
    }

    function kill() public {
        if (msg.sender == feeAddress) {
            selfdestruct(feeAddress);
        }
    }
}

在这个实例中，我们能够看到合约在使用随机数去挑选winner。address winningAddress = contestants[winningNumber].addr。也就是说在该函数中，系统会首先生成一个随机数，然后将随机数传递到contestants []中，从而选择出获胜者。倘若攻击者能够控制这个随机数，让随机数每次都生成为其自己的index是不是就可以无限作恶？那我们看一看具体的随机数是如何生成的。

address seed1 = contestants[uint(block.coinbase) % totalTickets].addr;

address seed2 = contestants[uint(msg.sender) % totalTickets].addr;

uint seed3 = block.difficulty;

bytes32 randHash = keccak256(seed1, seed2, seed3);

uint winningNumber = uint(randHash) % totalTickets;

address winningAddress = contestants[winningNumber].addr;

上述是关键函数，在该函数中我们发现随机数的生成是需要三个种子：seed1、seed2、seed3。而这三个种子分别由block.coinbase、msg.sender、block.difficulty生成，而这三个变量除了msg.sender之外，其余的均可在链上读取到。也就是说攻击者仅需要控制合约的地址就可以进行作恶。

四、竞赛随机数漏洞

下面我们来看几个CTF竞赛题目的解法。

首先我们看一道随机数预测的题目：

pragma solidity ^0.4.18;

contract CoinFlip {
  uint256 public consecutiveWins;
  uint256 lastHash;
  uint256 FACTOR = 57896044618658097711785492504343953926634992332820282019728792003956564819968;

  function CoinFlip() public {
    consecutiveWins = 0;
  }

  function flip(bool _guess) public returns (bool) {
    uint256 blockValue = uint256(block.blockhash(block.number-1));

    if (lastHash == blockValue) {
      revert();
    }

    lastHash = blockValue;
    uint256 coinFlip = blockValue / FACTOR;
    bool side = coinFlip == 1 ? true : false;

    if (side == _guess) {
      consecutiveWins++;
      return true;
    } else {
      consecutiveWins = 0;
      return false;
    }
  }
}

这个题目的要求我们猜对10次合约的内容。所以我们对合约进行部署：

contract Attack {
  CoinFlip fliphack;
  address instance_address = 0x2f99655a6ddfd3e13561acf2c1c724385bb6a80e;
  uint256 FACTOR = 57896044618658097711785492504343953926634992332820282019728792003956564819968;

  function Attack() {
    fliphack = CoinFlip(instance_address);
  }

  function predict() public view returns (bool){
    uint256 blockValue = uint256(block.blockhash(block.number-1));
    uint256 coinFlip = uint256(uint256(blockValue) / FACTOR);
    return coinFlip == 1 ? true : false;
  }

  function hack() public {
    bool guess = predict();
    fliphack.flip(guess);
  }

  function getbalance() view public returns(uint) {
      return fliphack.getbalance();
  }

  function getflag(string a) public{
      fliphack.CaptureTheFlag(a);
  }
}

我们对合约进行部署：

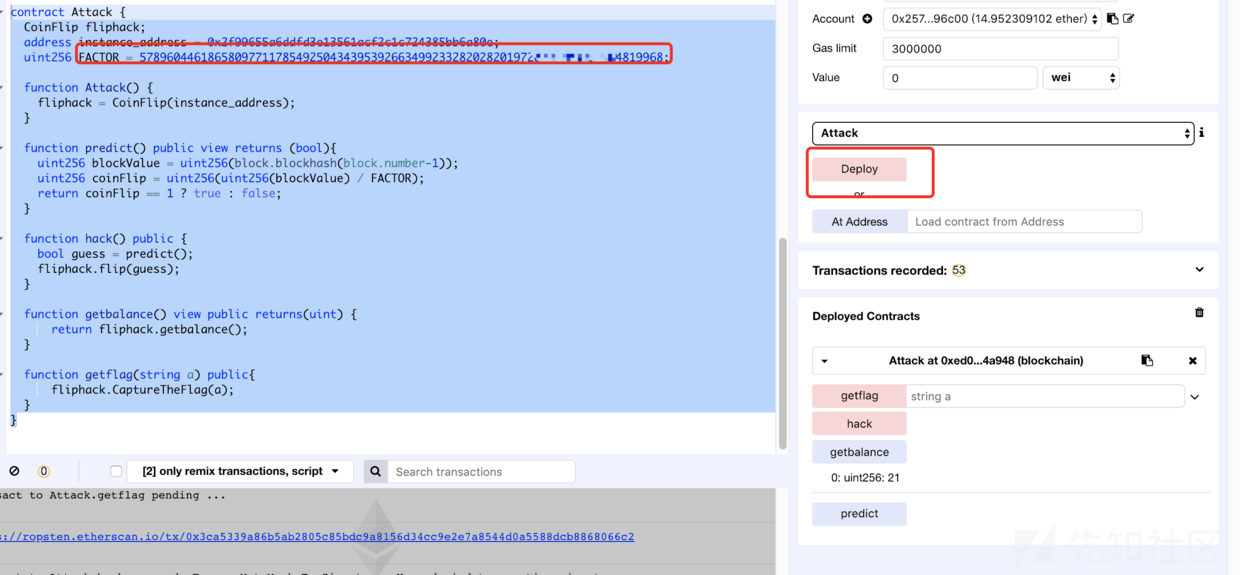
根据我们前面的分析，本题目中随机数预测使用的是block.blockhash(block.number-1)函数，而此函数是所有用户均可以从区块上读到。

所以我们的攻击合约直接从链上读取随机数种子即可完全还原随机数。

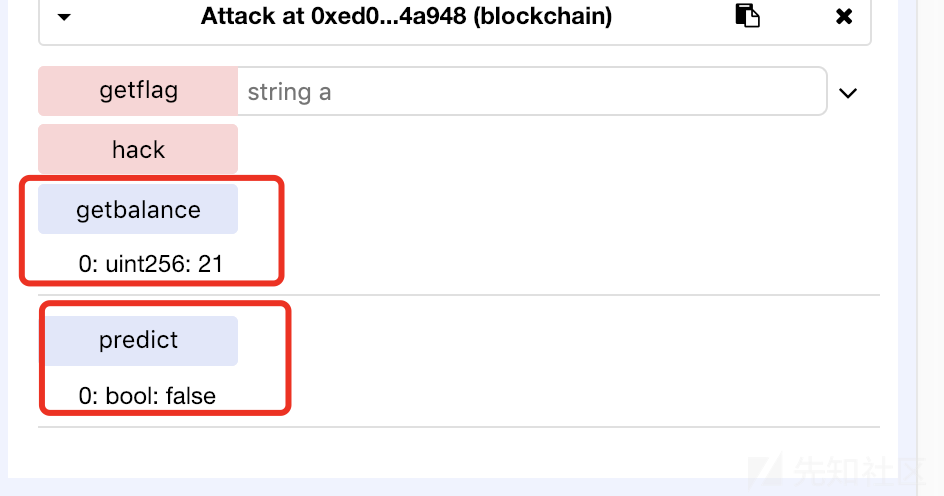
运行20次，得到预测次数。很简单的题目。

下面我们看一道LCTF2018中的ctf题目。

源代码如下：

//Welcome to LCTF
pragma solidity ^0.4.24;
library SafeMath {

    function mul(uint256 a, uint256 b) internal pure returns (uint256) {
        if (a == 0) {
            return 0;
        }

        uint256 c = a * b;
        require(c / a == b);

        return c;
    }

    function div(uint256 a, uint256 b) internal pure returns (uint256) {
        require(b > 0); 
        uint256 c = a / b;

        return c;
    }

    function sub(uint256 a, uint256 b) internal pure returns (uint256) {
        require(b <= a);
        uint256 c = a - b;

        return c;
    }

    function add(uint256 a, uint256 b) internal pure returns (uint256) {
        uint256 c = a + b;
        require(c >= a);

        return c;
    }
}


contract ERC20{
    using SafeMath for uint256;

    mapping (address => uint256) public balances;

    uint256 public _totalSupply;

    function totalSupply() public view returns (uint256) {
        return _totalSupply;
    }

    function balanceOf(address owner) public view returns (uint256) {
        return balances[owner];
    }

    function transfer(address _to, uint _value) public returns (bool success){
        balances[msg.sender] = balances[msg.sender].sub(_value);
        balances[_to] = balances[_to].add(_value);

        return true;
    }
}

contract ggToken is ERC20 {

    string public constant name = "777";
    string public constant symbol = "666";
    uint8 public constant decimals = 18;
    uint256 public constant _airdropAmount = 1000;

    uint256 public constant INITIAL_SUPPLY = 20000000000 * (10 ** uint256(decimals));

    mapping(address => bool) initialized;

    constructor() public {
        initialized[msg.sender] = true;
        _totalSupply = INITIAL_SUPPLY;
        balances[msg.sender] = INITIAL_SUPPLY;
    }


}


contract ggbank is ggToken{
    address public owner;
    mapping(uint => bool) locknumber;

    event GetFlag(
            string b64email,
            string back
        );

    modifier authenticate {
        require(checkfriend(msg.sender));_;
    }
    constructor() public {
        owner=msg.sender;
    }
    function checkfriend(address _addr) internal pure returns (bool success) {
        bytes20 addr = bytes20(_addr);
        bytes20 id = hex"000000000000000000000000000000000007d7ec";
        bytes20 gg = hex"00000000000000000000000000000000000fffff";

        for (uint256 i = 0; i < 34; i++) {
            if (addr & gg == id) {
                return true;
            }
            gg <<= 4;
            id <<= 4;
        }

        return false;
    }
    function getAirdrop() public authenticate returns (bool success){
         if (!initialized[msg.sender]) {
            initialized[msg.sender] = true;
            balances[msg.sender] = _airdropAmount;
            _totalSupply += _airdropAmount;
        }
        return true;
    }
    function goodluck()  public payable authenticate returns (bool success) {
        require(!locknumber[block.number]);
        require(balances[msg.sender]>=100);
        balances[msg.sender]-=100;
        uint random=uint(keccak256(abi.encodePacked(block.number))) % 100;
        if(uint(keccak256(abi.encodePacked(msg.sender))) % 100 == random){
            balances[msg.sender]+=20000;
            _totalSupply +=20000;
            locknumber[block.number] = true;
        }
        return true;
    }


    function PayForFlag(string b64email) public payable authenticate returns (bool success){

            require (balances[msg.sender] > 200000);
            emit GetFlag(b64email, "Get flag!");
        }
}

我们看获得flag的条件是需要require (balances[msg.sender] > 200000)。

function getAirdrop() public authenticate returns (bool success){
         if (!initialized[msg.sender]) { //空投
            initialized[msg.sender] = true;
            balances[msg.sender] = _airdropAmount;
            _totalSupply += _airdropAmount;
        }
        return true;
    }

在上面的函数中我们知道每一个新用户都会获得uint256 public constant _airdropAmount = 1000;1000的钱。然而，我们看到goodluck函数中能够看到：

function goodluck()  public payable authenticate returns (bool success) {
    require(!locknumber[block.number]); //判断block.numbrt
    require(balances[msg.sender]>=100); //余额大于100
    balances[msg.sender]-=100; //每次调用要花费100token
    uint random=uint(keccak256(abi.encodePacked(block.number))) % 100; //随机数
    if(uint(keccak256(abi.encodePacked(msg.sender))) % 100 == random){ //随机数判断
        balances[msg.sender]+=20000;
        _totalSupply +=20000;
        locknumber[block.number] = true;
    }
    return true;
}

我们看到这里就是随机数预测。而在这个随机数预测中我们使用了abi.encodePacked(msg.sender)与random=uint(keccak256(abi.encodePacked(block.number))) % 100。也就是说我们需要这两个数相等即可返回ture。

而msg.sender可以直接控制已知的地址，那么左值就是已知的，剩下的就是要等待一个右值出现，由于block.number是自增的，我们可以通过提前计算出一个block.number，然后写脚本监控这个值出现，提前开始发起交易抢打包，就能够返回true了。

我们可以查看此题目的wp。

五、参考资料

本稿为原创稿件，转载请标明出处。谢谢。