CTFtime平台上发现的一场比赛,记录一下其中的2道逆向题
Feed_me
题目打开,发现一个scanf("%s",s),明显有栈溢出倾向,而IDA将变量识别如下

注意后面的三个atoi,后两个的参数比较迷,相对s的偏移分别为10和20,这里我把s的类型重新定义为char s[30]
因为这题保护全开,不是考察pwn,应该是考察栈上变量偏移的识别
那么我们输入的字符串每10个字符被解析成3个int型数据
主要的判断可以看做三元一次方程
input1 + input2 = num1
input2 + input3 = num2
input3 + input1 = num3
=>
input1 = num1 + num3 - num2 / 2
input2 = num1 + num2 - num3 / 2
input3 = num2 + num3 - num1 / 2
多说一句,解方程时把三个式子加起来除以二后,分别减去每一个式子,即可得到方程的解
根据srand(time(0))和rand()的特性:随机种子确定,生成的序列也确定,写出python脚本扔程序跑就可以了
但是我不太熟悉python对rand的处理,直接C程序跑出来,手动喂给程序了
补充
解题过程中有一些想法
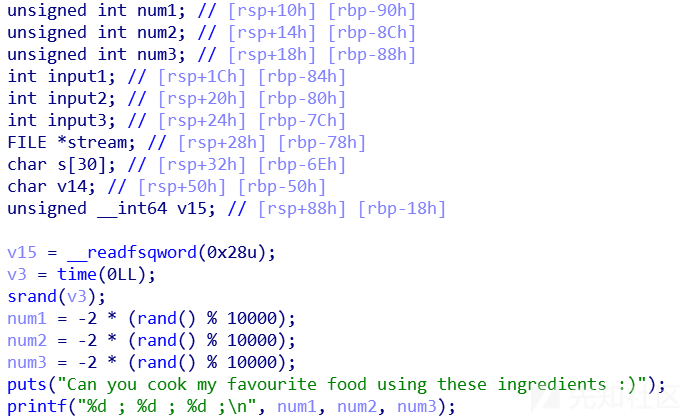
这里num1,num2,num3都是unsigned int,而它们都被以%d的形式输出
因为rand()返回值为int型,但是必定返回一个正数,模10000后再乘以-2,相当于把一个绝对值很小的负数赋值给了unsigned int
以%d有符号数输出结果,是三个负数,是应该的

可是num系列数据的实际类型是无符号的,是一个很大的正数
而我们输入的字符串被解析成了3个int数据,而且都是负数,在判断时,如何比较一个正unsigned int和负int?
看一下汇编代码

2个int数据add后与unsigned int比较,实际上应该是比较的二进制数据
只要二进制的32个bit相等,那么就判断相等
做一个小实验
#include<stdio.h>
#include<stdlib.h>
int main(int argc,char**argv){
int num1 = -1;
unsigned int num2 = -1;
if(num1==num2){
printf("num1==num2");
}
return 0;
}
num1就是单纯的-1,而num2会是0xffffffff,是一个大正数
实际上if判断为真,会输出num1==num2
发现这个问题的原因主要是,我本地写C代码测试时,发现以
%d输出预期的值input1、input2、input3时,都是长度为10的int数据,而连起来就是30长度的纯数字字符串,这不能被atoi识别,超过范围会返回-1,于是有了上文的一些想法,发现原来是二进制比较的问题
Super Secure Vault
IDA打开,主逻辑如下

发现函数名都在,而且getNum和mod函数都接收了一个字符串作为参数,实际上是指向字符串的指针
先看一下getNum函数

它的作用实际上是从字符串中取出一段数据并返回int64型
mod函数的行为也和名字一样

注意到程序虽然用了scanf,但是保护全开,也就没有REpwn这种要改数据的可能性了,输入的长度姑且认为是30
因为getNum返回的值不受我们输入字符串的影响,只要动态调出来就可以了
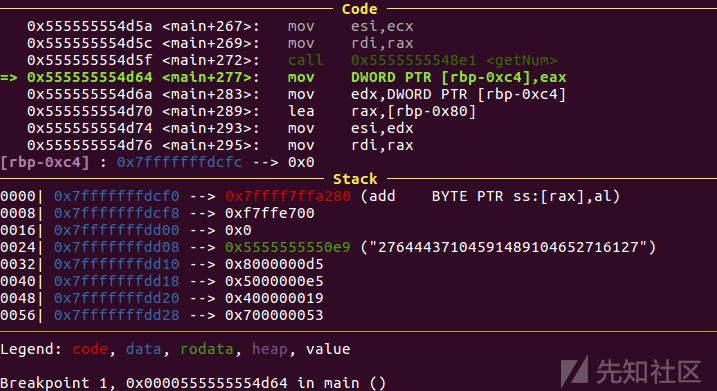
比如第一个值是27644437,要求input % 27644437 == 213
同样的,可以得出以下5个线性同余方程组
input % 27644437 == 213
input % 10459 == 229
input % 1489 == 25
input % 1046527 == 83
input % 16127 == 135
和中国剩余定理有关,网上找个脚本解一下
from functools import reduce
def egcd(a, b):
if 0 == b:
return 1, 0, a
x, y, q = egcd(b, a % b)
x, y = y, (x - a // b * y)
return x, y, q
def Chinese_remainder(pairs):
mod_list, remainder_list = [p[0] for p in pairs], [p[1] for p in pairs]
mod_product = reduce(lambda x, y: x * y, mod_list)
mi_list = [mod_product//x for x in mod_list]
mi_inverse = [egcd(mi_list[i], mod_list[i])[0] for i in range(len(mi_list))]
x = 0
for i in range(len(remainder_list)):
x += mi_list[i] * mi_inverse[i] * remainder_list[i]
x %= mod_product
return x
if __name__=='__main__':
print(Chinese_remainder([(27644437, 213), (10459, 229), (1489, 25),(1046527,83),(16127,135)]))
出结果:

长度也符合要求,是一个符合条件的解
然后我们就被要求输入password
主要逻辑在func2中

我们第一轮输入的字符串会被追加"27644437104591489104652716127"
再被追加0x3038和\x00

然后基本就是查表了,由于程序开了PIE,我不知道怎么用angr秒解它,于是只能patch程序,用gdb下断点看了

这里把两行中的!=改成了==,并且下断点观察矩阵中给出的值
密码随便输入!!!!!!!!!!!!!!
然后RAX中的值,也就是cmp cl,al中会给出应该输入的字符
收集一下就是:pctf{R3v3rS1Ng_#s_h311_L0t_Of_Fun}
我猜测程序中可能是手动把符合同余方程组的解都算了一遍?然后把数据填入那个巨型矩阵?
最后其他位置乱放了一些字符?
总结一下
这两道题的基本是一个递进的关系,其中第二题的函数编写值得学习一下,C语言如何处理这种大数的mod,之前我没有仔细想过,这段代码实现也没有彻底的理解......
-
 Pragyan CTF 19 binary.rar
下载
Pragyan CTF 19 binary.rar
下载
 转载
转载
 分享
分享

