前言
0ctf这道题目其实不需要对抗算法就能做出来了,主要是出题人抬了一手误差范围给大了。
虽然给了很多文件,不过其实大多数都没有用。
核心部分就是python flask框架搭建的web,keras搭建的神经网络,内置了训练好的h5模型。
所以tensorflow,keras,flask, numpy这些基本环境都需要安装,安装过程直接百度即可。
分析
查看app.py
核心函数index:
def index():
if request.method == 'POST' and request.form["submit"]==u"upload":
try:
f = request.files['file']
with zipfile.ZipFile(f) as myzip, tempfile.TemporaryDirectory() as t_dir, graph.as_default():
lenet = LeNet() # 导入训练好的LeNet模型
for i in range(8): # 依次static的八张图片以及上传的八张图片
pathori = os.path.join(DIR, "static", "%d.jpg" % i)
path = os.path.join(t_dir, "%d.jpg" % i)
with myzip.open("%d.jpg" % i, "r") as ii:
with open(path, "wb") as oo:
oo.write(ii.read())
imageori = plt.imread(pathori) # 图片转化成矩阵形式 shape为(32, 32, 3)
imagenew = plt.imread(path)
# 计算图片被修改的误差,每个像素点的差值的平方的和的平均值
err = mse(imageori,imagenew)
print(err)
# 误差在0-200内才用模型对其预测
if err<200 and err!=0:
predictid, predictclass, _ = predictimg(path,lenet)
predictidori, predictclassori, _ = predictimg(pathori,lenet)
print(predictclass, predictclassori)
if predictid == predictidori:
name = "id:%d your result is " % i + predictclass
break
# 两张图片预测结果不相同则进入下一轮循环
else:
continue
elif err!=0:
name ="id:%d error too much modification, %s" % (i, err)
break
else:
name ="id:%d please do something" % i
break
# 八张图片全部与原有图片预测结果不同,则返回flag
else:
name = "flag{FLAG}"
except Exception as e:
name = "error %s" % e
else:
name = ""
return render_template('index.html', name=name,time_val=time.time())
通过分析可以得知:
程序需要你上传八张图片的压缩包
你的每一张图片都必须是基于static文件夹中的基础图片0-7生成的,误差有一定的约束(mse()函数计算)
你的上传图片不能被识别成它基础图片的同一种类
预测图片分类调用了predicting函数,发现confidence其实是softmax后的结果,可以理解成模型对传入图片被识别成各个种类的置信度。置信度最大的对应位置其实就是模型最后对图片识别的结果:
def predictimg(path,lenet):
image = plt.imread(path)
confidence = lenet.predict(image)[0]
predicted_class = np.argmax(confidence)
return predicted_class, class_names[predicted_class],confidence[predicted_class]
可以在同目录下建一个test.py测试一下
def predictimg(path, lenet):
image = plt.imread(path)
confidence = lenet.predict(image)[0] # 得到lenet模型预测对每种类别的置信度
predicted_class = np.argmax(confidence)
for i in range(10):
print(class_names[i], confidence[i] * 100)
return predicted_class, class_names[predicted_class], confidence[predicted_class]
DIR = os.path.abspath(os.path.dirname(__file__))
path = DIR + "\\static\\0.jpg"
lenet = LeNet()
image_a = plt.imread(path)
pre_class, pre_name, _ = predictimg(path, lenet)
print("predict name: ", pre_name)
输出了分类以及置信度
Successfully loaded lenet
airplane 59.14044976234436
automobile 0.0004856942268816056
bird 37.361788749694824
cat 1.458375621587038
deer 1.07676163315773
dog 0.8214056491851807
frog 0.0049890899390447885
horse 0.11071392800658941
ship 0.0228012926527299
truck 0.002230720747320447
predict name: airplane
再看一下lenet.predict函数,在networks文件夹里的lenet.py:
def predict(self, img):
processed = self.color_process(img)
return self._model.predict(processed, batch_size=self.batch_size)
def color_process(self, imgs):
if imgs.ndim < 4:
imgs = np.array([imgs])
imgs = imgs.astype('float32')
mean = [125.307, 122.95, 113.865]
std = [62.9932, 62.0887, 66.7048]
for img in imgs:
for i in range(3):
img[:, :, i] = (img[:, :, i] - mean[i]) / std[i]
return imgs
用color_process对每一个像素点都操作了一下,训练时也是这么操作的,所以不用在意。
然后调用_model_predict进行预测
查看上面的代码可知,_model 是加载的训练好的模型, 在models文件夹下的lenet.h5
model的predict是keras训练好后的模型自带的函数,用来输出预测概率的。
简单解法
这种解法简单好理解,但是不怎么具有通用性。
因为要求我们的上传的图片像素的平均误差平方不超过200,所以每个像素的变化范围很大,变化意味着置信度发生变化。
同时常识告诉我们,扰动施加的越大,那么识别误差也一定会越大。
修改一下predicting,然后测试一下:
class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
def predictimg(path, lenet, judge=False, data=None):
if judge:
image = data
else:
image = plt.imread(path)
confidence = lenet.predict(image)[0] # 得到lenet模型预测对每种类别的置信度
predicted_class = np.argmax(confidence)
for i in range(10):
print(class_names[i], confidence[i] * 100)
return predicted_class, class_names[predicted_class], confidence[predicted_class]
def mse(imageA, imageB):
err = np.sum((imageA.astype("float") - imageB.astype("float")) ** 2)
err /= float(imageA.shape[0] * imageA.shape[1])
return err
lenet = LeNet()
image_b = np.zeros(shape=(32, 32, 3), dtype=np.float32)
rd = np.random.rand(32, 32, 3) * 14
DIR = os.path.abspath(os.path.dirname(__file__))
path = DIR + "\\static\\0.jpg"
image_a = plt.imread(path)
image_b = image_a.astype(np.float32) + rd
print("error: ", mse(image_a, image_b))
pre_class1, pre_name, _ = predictimg(path, lenet)
print("predict name: ", pre_name)
print("-" * 20)
pre_class2, pre_name, _ = predictimg(path, lenet, judge=True, data=image_b)
print("predict name: ", pre_name)
输出:
Successfully loaded lenet
error: 195.31106524999055
airplane 59.14044976234436
automobile 0.0004856942268816056
bird 37.361788749694824
cat 1.458375621587038
deer 1.07676163315773
dog 0.8214056491851807
frog 0.0049890899390447885
horse 0.11071392800658941
ship 0.0228012926527299
truck 0.002230720747320447
predict name: airplane
--------------------
airplane 45.86603343486786
automobile 0.0005276419415167766
bird 50.21917223930359
cat 0.9045490995049477
deer 2.296214923262596
dog 0.5382389295846224
frog 0.005475602301885374
horse 0.12820508563891053
ship 0.03867906052619219
truck 0.0029019753128523007
predict name: bird
仅仅是加了一些随机的干扰,就使得图片在误差允许范围内从airplane被识别成了bird。
为了不动脑,生成这种随机扰动就很好!!
同时根据我学习对抗样本的经验,施加了如下的扰动,没什么科学依据,只是这样随机性更大:
rd = np.random.rand(32, 32, 3).astype(np.float32)
rd1, rd2 = rd, rd
rd1 = rd1 * (rd1 > 0.5) * -1
rd2 = rd2 * (rd2 < 0.5)
rd = (rd1 + rd2) * 14
然后构造如下脚本来生成我们需要的对抗样本:
final_image = []
n = 0
for i in range(8):
image_b = np.zeros(shape=(32, 32, 3), dtype=np.float32)
pre_class1 = 0
pre_class2 = 0
while pre_class1 == pre_class2:
rd = np.random.rand(32, 32, 3).astype(np.float32)
rd1, rd2 = rd, rd
rd1 = rd1 * (rd1 > 0.5) * -1
rd2 = rd2 * (rd2 < 0.5)
rd = (rd1 + rd2) * 14
path = DIR + "\\static\\{}.jpg".format(i)
image_a = plt.imread(path)
image_b = image_a.astype(np.float32) + rd
if mse(image_a, image_b) > 200:
continue
n += 1
pre_class1, pre_name, _ = predictimg(path, lenet)
pre_class2, pre_name, _ = predictimg(path, lenet, judge=True, data=image_b)
print("---adv image %d success---" % i)
print("---error: %f---" % mse(image_a, image_b))
print("---{} loops---".format(n))
final_image.append(image_b)
class1 = []
class2 = []
for i in range(8):
path = DIR + "\\static\\{}.jpg".format(i)
pre_class1, pre_name, _ = predictimg(path, lenet)
class1.append(pre_class1)
for i in range(8):
pre_class2, pre_name, _ = predictimg(path, lenet, judge=True, data=final_image[i])
class2.append(pre_class2)
print(class1)
print(class2)
from PIL import Image
for i in range(8):
im = Image.fromarray(final_image[i].astype(np.uint8))
name = "{}.jpg".format(i)
im.save(name)
print("Done!"")
结果
Successfully loaded lenet
---adv image 0 success---
---error: 196.508524---
---2 loops---
---adv image 1 success---
---error: 199.452623---
---4 loops---
---adv image 2 success---
---error: 198.868474---
---9 loops---
---adv image 3 success---
---error: 193.501790---
---10 loops---
---adv image 4 success---
---error: 197.218088---
---1218 loops---
---adv image 5 success---
---error: 193.843418---
---1226 loops---
---adv image 6 success---
---error: 193.986569---
---1473 loops---
---adv image 7 success---
---error: 195.061129---
---3890 loops---
[0, 7, 6, 0, 4, 1, 9, 6]
[2, 6, 3, 6, 2, 3, 7, 4]
Done!
运气好一点差不多循环4000次左右就能运行完毕。
从两个预测结果来看 预测结果已经被我们全部修改成功,再把这些图片打包成一个zip传上去就行了。
最后结果没办法展示了,可能是我在windows端做的原因,tempfile模块始终有一些莫名其妙的问题,上传zip文件后总会出现一些问题。
给的扰动范围大的话,可以用这种随机方法莽出来,不过我们还是要寻求一个正规做法。
正规解法:
先介绍一下FGSM(fast gradien sign method):
是由Lan Goodfellow等人提出的。
论文:https://arxiv.org/abs/1412.6572.
公式:
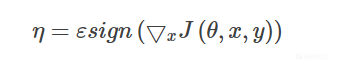
- sign:符号函数(正数输出1,负数输出-1)
- x:输入的图像矩阵
- y:预测值
- J:损失函数,常为交叉熵
- $\theta$ : 模型的参数
- $\epsilon$ : 一个较小的扰动权重参数
- $\eta$ : 最终向图像施加的扰动
直观的理解就是向图象是加了一个肉眼难辨的噪声,导致其模型的损失函数顺着梯度方向增大,这样样本的损失值就会增大,导致其预测结果会越过决策边界,从而被模型错误分类。
想了解更多请阅读论文,毕竟我也是工具化的学习,理解并不深。
所以我们需要以下几个参数:
损失函数,输入,预测值,正常结果,损失函数对输入的梯度。
这里用keras.backend来实现,这个模块可以获取模型中间层的各种参数,很强大的模块。
参考了 https://ctftime.org/writeup/13801 的写法
image_a = plt.imread(path).astype(np.float32)
image_a = color_process(image_a)
tmp = image_a
TARGET = np.argmax(model.predict(tmp)[0])
target = np.zeros(10)
target[TARGET] = 1
session = K.get_session()
d_model_d_x = K.gradients(keras.losses.categorical_crossentropy(target, model.output), model.input)
eval_grad = session.run(d_model_d_x, feed_dict={model.input: image_a})[0][0]
为了保险起见,我在其中加上了随机扰动的保险,不过事实证明根本不需要。
model = load_model("./networks/models/lenet.h5")
n = 0
DIR = os.path.abspath(os.path.dirname(__file__))
eps = 1
for i in range(8):
path = DIR + "\\static\\{}.jpg".format(i)
image_a = plt.imread(path).astype(np.float32)
image_a = color_process(image_a)
tmp = image_a
TARGET = np.argmax(model.predict(tmp)[0])
target = np.zeros(10)
target[TARGET] = 1
session = K.get_session()
d_model_d_x = K.gradients(keras.losses.categorical_crossentropy(target, model.output), model.input)
while np.argmax(model.predict(image_a)[0]) == TARGET:
eval_grad = session.run(d_model_d_x, feed_dict={model.input: image_a})[0][0]
fgsm = np.sign(eval_grad * eps)
image_a = image_a + fgsm
err = mse(image_a, tmp)
n += 1
if n % 1000 == 0:
print("loops: ", n)
if err > 200:
rd = np.random.rand(32, 32, 3).astype(np.float32)
rd1, rd2 = rd, rd
rd1 = rd1 * (rd1 > 0.5) * -1
rd2 = rd2 * (rd2 < 0.5)
rd = (rd1 + rd2)
image_a = tmp + rd * (n / 1000)
continue
err = mse(image_a, tmp)
print("error: {}, loop: {}".format(err, n))
pre = np.argmax(model.predict(tmp)[0])
now = np.argmax(model.predict(image_a)[0])
conf_pre = model.predict(tmp)[0][pre]
conf_now = model.predict(image_a)[0][now]
print("{}.{}:{} ====> {}.{}:{}".format(pre, class_names[pre], conf_pre*100,
now, class_names[now], conf_now*100))
print("-"*60)
结果在平均扰动值95左右,就可以实现样本的误判,而且每次生成对抗样本仅仅需要一轮。
error: 95.24999996137205, loop: 1
0.airplane:59.14044976234436 ====> 6.frog:96.1998999118805
------------------------------------------------------------
error: 95.90625007138824, loop: 2
7.horse:69.32011842727661 ====> 6.frog:99.58266615867615
------------------------------------------------------------
error: 95.90624985010452, loop: 3
6.frog:35.53158938884735 ====> 3.cat:46.78606688976288
------------------------------------------------------------
error: 95.90624998283977, loop: 4
0.airplane:53.729891777038574 ====> 9.truck:88.66733312606812
------------------------------------------------------------
error: 95.62500006915087, loop: 5
4.deer:95.75170874595642 ====> 6.frog:67.56904721260071
------------------------------------------------------------
error: 95.15625016653229, loop: 6
1.automobile:90.84147810935974 ====> 7.horse:83.24228525161743
------------------------------------------------------------
error: 95.71874987221618, loop: 7
9.truck:77.83461213111877 ====> 5.dog:98.84703159332275
------------------------------------------------------------
error: 95.99999997530912, loop: 8
6.frog:91.78876280784607 ====> 7.horse:43.60279738903046
------------------------------------------------------------
再把数据转化成图片就可以了!
题目以及解题的脚本我就传到附件了。
参考
https://arxiv.org/abs/1412.6572
https://ctftime.org/writeup/13801
-
 neuron_solve.zip
下载
neuron_solve.zip
下载

 转载
转载
 分享
分享

没有评论