引言

Stephen Dolan 在他的论文《mov is Turing-complete》中提出了一个有趣的观点：x86 架构中的 mov 指令本身可以构建一个图灵机，从而证明它是图灵完备的（Turing-complete）。图灵完备性是一个系统能够模拟任何图灵机的能力，这意味着它可以执行任何算法。
这篇论文的核心观点是，尽管 mov 指令通常被看作是一个简单的数据传输指令，但它实际上可以用来实现更复杂的计算。以下是一些关键点，概述了这篇论文的主要内容：
图灵完备性的定义：首先，论文定义了图灵完备性，即一个系统能够模拟任何图灵机的能力。
x86架构的mov指令：mov 指令用于在 x86 架构中移动数据，可以是将立即数移动到寄存器，或者在寄存器之间移动数据。
mov指令的局限性：Dolan 指出，尽管 mov 指令在表面上看起来功能有限，但它可以通过特定的方式组合使用来实现更复杂的操作。
构建图灵机：论文中展示了如何仅使用 mov 指令来构建一个简单的图灵机。这包括使用寄存器来模拟图灵机的带子（tape）和头部（head）。
实现基本操作：Dolan 展示了如何使用 mov 指令来实现图灵机的基本操作，如移动头部、读写带子上的符号。
证明：通过构建一个具体的图灵机模型，并展示如何用 mov 指令来实现它的操作，Dolan 证明了 mov 指令的图灵完备性。
实际应用：虽然这个证明在理论上很有趣，但在实际编程中，我们通常不会只用 mov 指令来实现复杂的算法，因为这会非常低效和难以维护。
对计算理论的影响：这个发现对计算理论有一定的影响，因为它扩展了我们对图灵完备性的理解，并挑战了我们对简单指令潜在能力的看法。
这篇论文是计算理论领域的一个有趣贡献，它提醒我们即使是最基本的指令，也可能隐藏着实现复杂计算的能力。然而，这并不意味着在实际编程实践中，我们应该尝试只用 mov 指令来解决问题。实际上，这样做会非常繁琐且不实用。
换句话说,就是一个程序,可以完全由mov指令完成,对的,你没有听错,不带有任何的其他指令(可以有一些jmp?)
在逆向分析中,我们一般称之为movfuscator代码混淆

例题分析

这里我发现了一道根据这个论文的题
XCTF-re5-packed-movement
我们以这道题为例进行探讨
通过die查壳

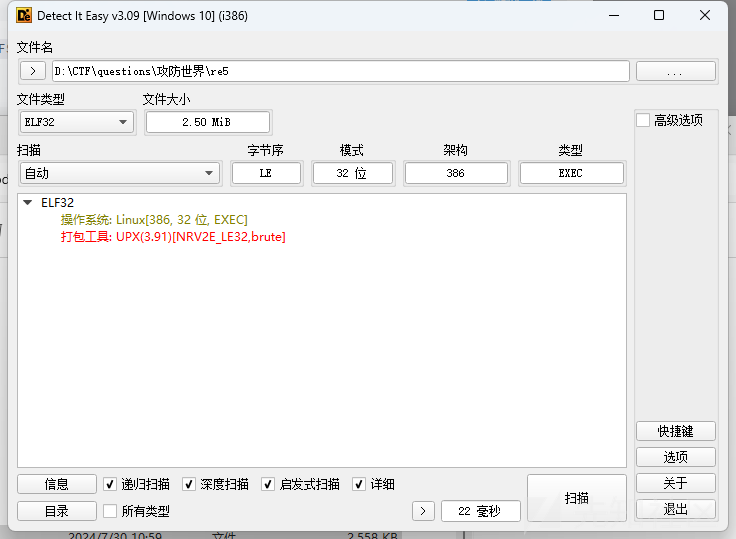
我们可以看见附加了upx壳
这里我选择使用upx.exe 进行脱壳操作

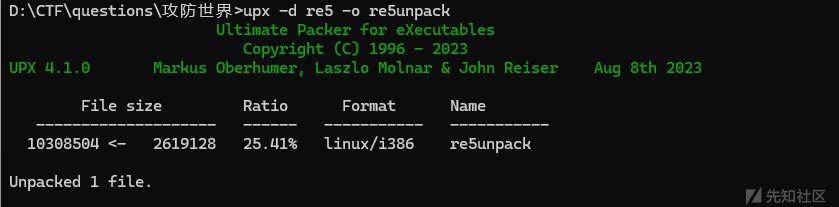
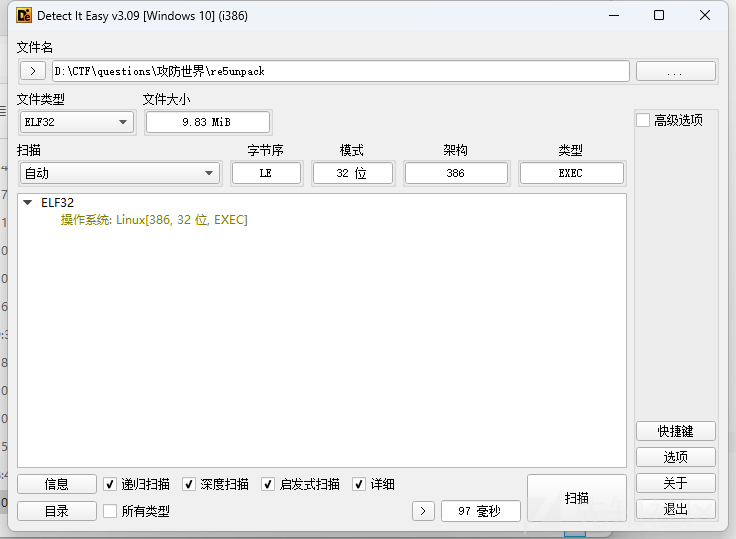
脱壳成功
32位IDA打开分析程序

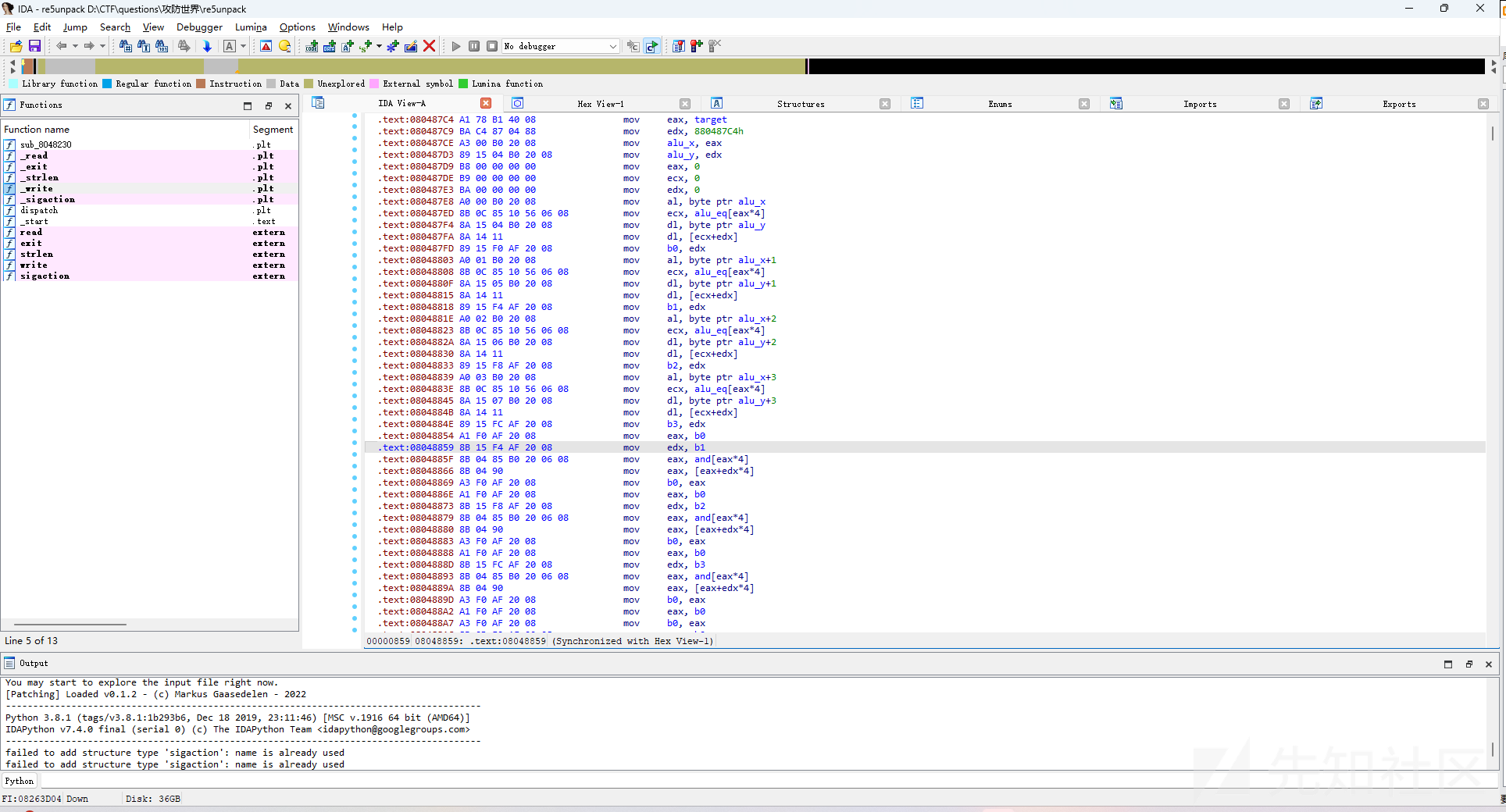
进去之后可以看见
汇编指令全是mov!

同时我们F5也会发现无法反编译

我们F12查看字符串,可以明显看见wrong 和ring的标志
我们找到right地址 ,尝试angr符号执行

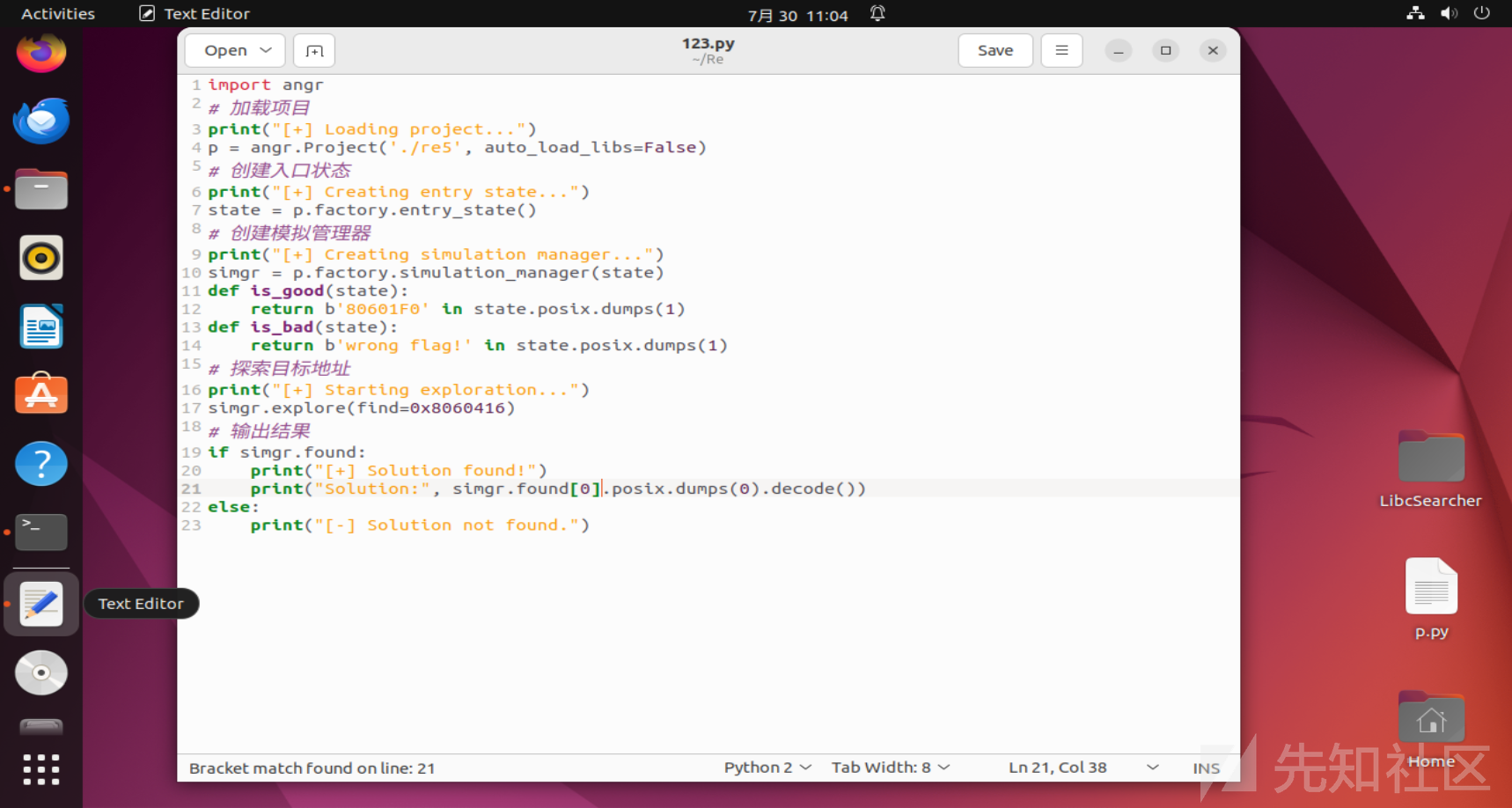
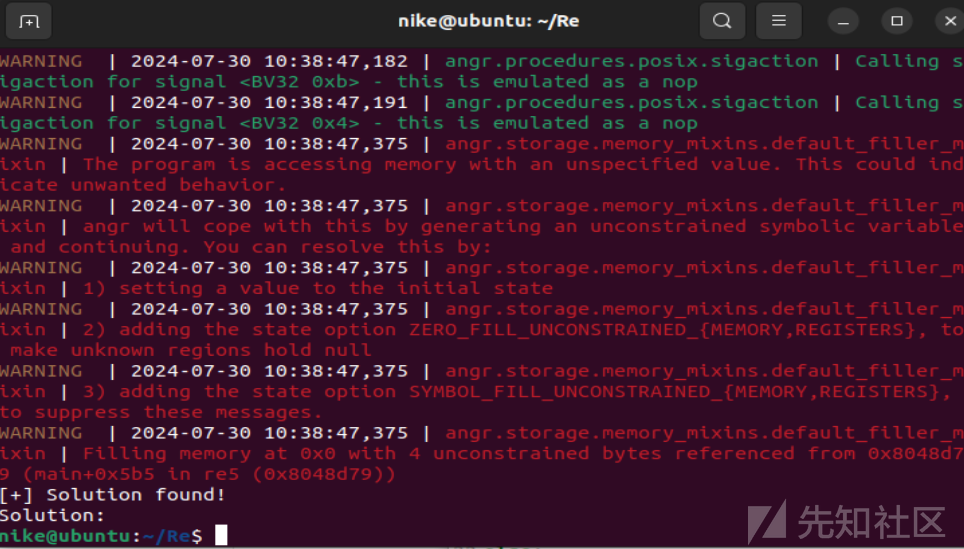
可惜最后不知道为什么,并没有任何回显操作,可能是mov混淆对angr也造成了影响

这个时候,其实大家细心可以发现前面的引言有一段话
"这篇论文是计算理论领域的一个有趣贡献，它提醒我们即使是最基本的指令，也可能隐藏着实现复杂计算的能力。然而，这并不意味着在实际编程实践中，我们应该尝试只用 mov 指令来解决问题。实际上，这样做会非常繁琐且不实用。"
这意味着,这篇程序无法进行大规模的加密解密以及反调试等
基本上大多数都是只能简单的拿flag进行逐步cmp
我们从查看wrong的引用,也可以大概猜出

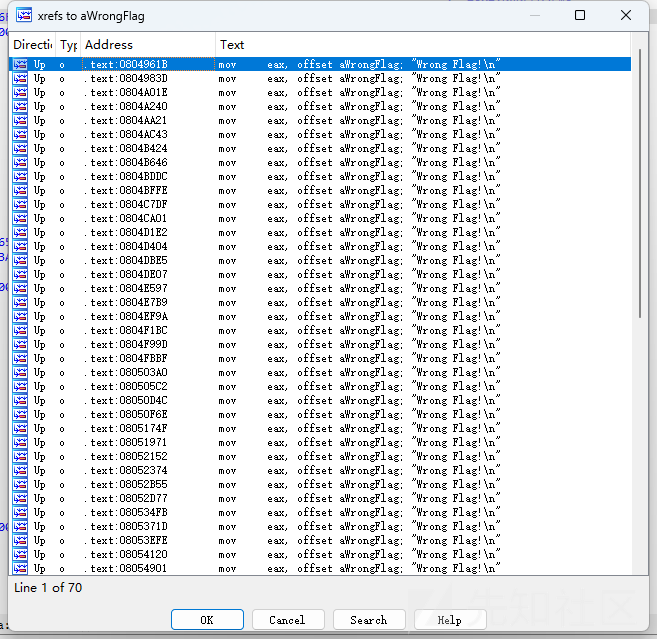
既然这么多wrong,而且都集中在相近的地址段
我们汇编去查看一下

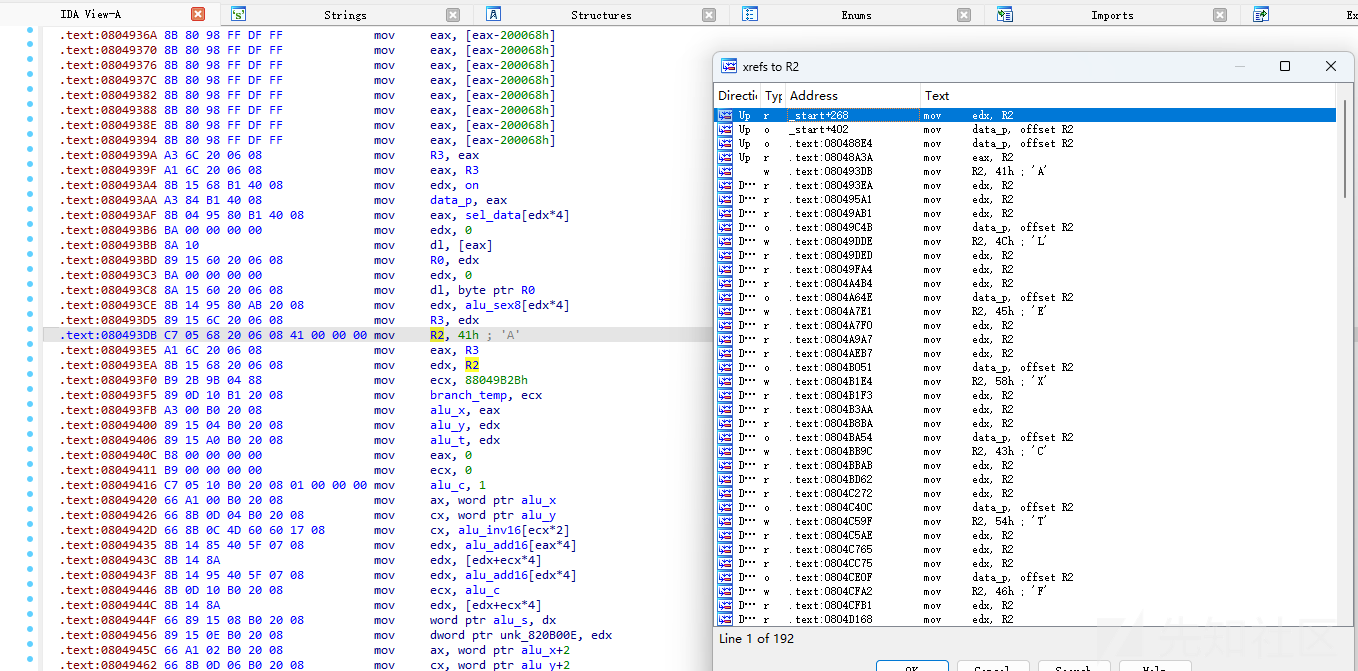
这里因为有一个41h被检测出来是可读字符串
我们X查看一下R2,很明显,这里就是flag
观察可以发现
C7 05 68 20 06 08
前面6位是固定操作数
41
后面一位是我们要的答案
IDA python 编写脚本

import idaapi
import idc

def clear(start_ea, end_ea):
    target_sequence = bytes([0xC7, 0x05, 0x68, 0x20, 0x06, 0x08])
    while start_ea < end_ea:
        # 获取6个字节
        byte_sequence = idc.get_bytes(start_ea, 6)
        # 检查是否与target_sequence匹配
        if byte_sequence == target_sequence:
            # 获取匹配序列后的第一个字节
            next_byte = idc.get_wide_byte(start_ea + 6)
            print(chr(next_byte), end='')
        start_ea += 1

# 定义起始和结束地址
start_ea = 0x80493DB
end_ea = 0x0805F8D6 

# 调用函数
clear(start_ea, end_ea)
print("ok")

shift +F12 运行

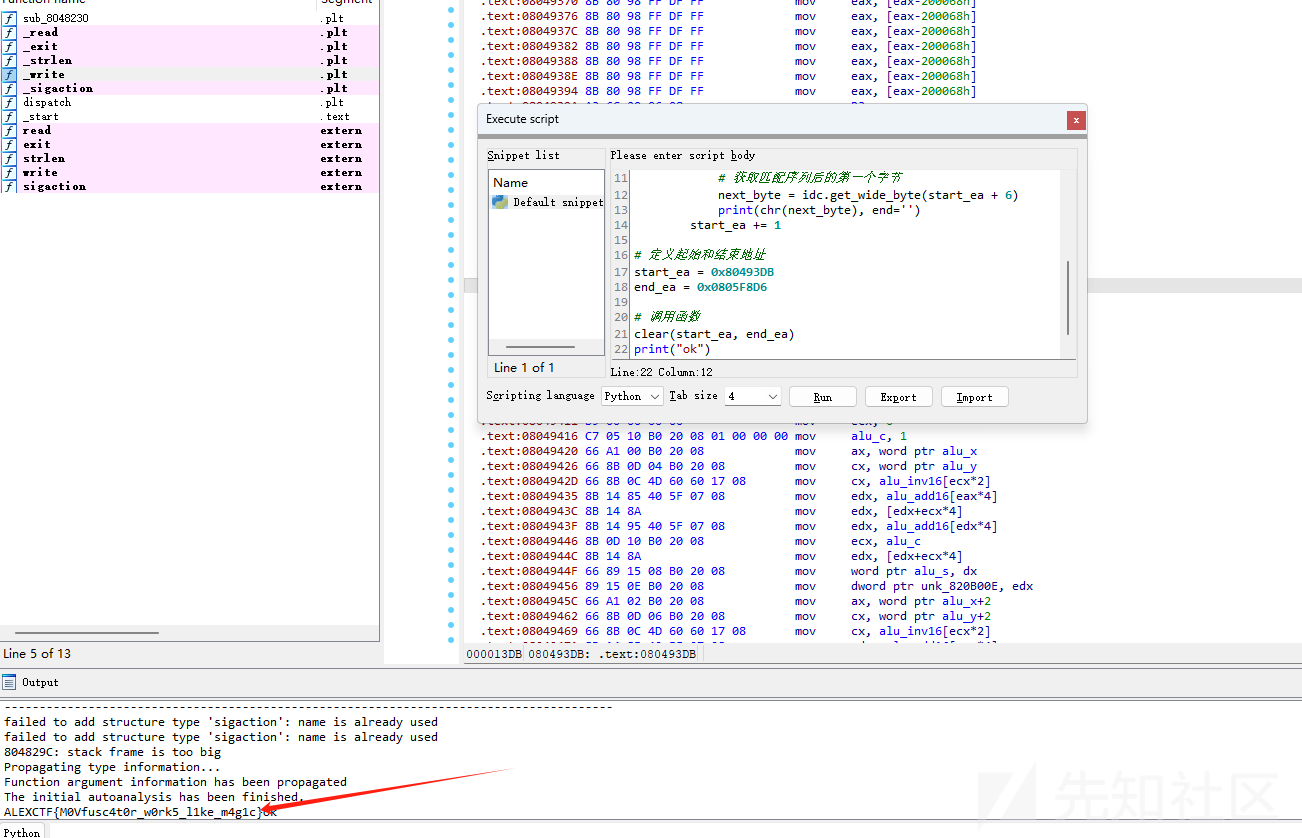
bingo!

总结

遇见了mov混淆,IDA会无法F5,但是这个时候由于mov混淆的局限性,整个程序逻辑必定是比较简单的,我们通过一下试探和猜测,锁定特征,来解出答案